题目内容
已知公差不为零的等差数列{an}的a2,a3,a14恰好构成一个等比数列,前7项和为S7=49,且对于任意的正整数n,都有b1+2b2+…+2n-1 bn=nan
(1)求数列{an},{bn}的通项公式.
(2)记{bn}的前n项和为Tn,求满足Tn>9的n的集合.
(1)求数列{an},{bn}的通项公式.
(2)记{bn}的前n项和为Tn,求满足Tn>9的n的集合.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)由已知得
,从而求出an=
-
.由b1+2b2+…+2n-1 bn=nan=
,得b1+2b2+…+2n-2bn-1=
,由此能求出bn=
.
(2)由bn=
,利用错位相减法求出Tn=
-
<
,由此能求出满足Tn>9的n的集合.
|
| 10n |
| 3 |
| 19 |
| 3 |
| 10n2-19n |
| 3 |
| 10(n-1)2-19(n-1) |
| 3 |
| 20n-29 |
| 3•2n-1 |
(2)由bn=
| 20n-29 |
| 3•2n-1 |
| 22 |
| 3 |
| 20n+11 |
| 3×2n-1 |
| 22 |
| 3 |
解答:
解:(1)∵公差不为零的等差数列{an}的a2,a3,a14恰好构成一个等比数列,前7项和为S7=49,
∴
,解得a1=-3,d=
,
∴an=-3+(n-1)×
=
-
.
∵b1+2b2+…+2n-1 bn=nan=
,
∴b1+2b2+…+2n-2bn-1=
,
∴2n-1bn=
-
=
,
∴bn=
.
(2)∵bn=
,
∴Tn=
+
+
+…+
,①
Tn=
+
+
+…+
,②
①-②,得:
Tn=-3+
+
+…+
-
=-3+
(
+
+…+
)-
=-3+
×
-
=
-
-
,
∴Tn=
-
<
,
∴满足Tn>9的n的集合为∅.
∴
|
| 10 |
| 3 |
∴an=-3+(n-1)×
| 10 |
| 3 |
| 10n |
| 3 |
| 19 |
| 3 |
∵b1+2b2+…+2n-1 bn=nan=
| 10n2-19n |
| 3 |
∴b1+2b2+…+2n-2bn-1=
| 10(n-1)2-19(n-1) |
| 3 |
∴2n-1bn=
| 10n2-19n |
| 3 |
| 10(n-1)2-19(n-1) |
| 3 |
| 20n-29 |
| 3 |
∴bn=
| 20n-29 |
| 3•2n-1 |
(2)∵bn=
| 20n-29 |
| 3•2n-1 |
∴Tn=
| -9 |
| 3 |
| 11 |
| 3×2 |
| 31 |
| 3×22 |
| 20n-29 |
| 3×2n-1 |
| 1 |
| 2 |
| -9 |
| 3×2 |
| 11 |
| 3×22 |
| 31 |
| 3×23 |
| 20n-29 |
| 3×2n |
①-②,得:
| 1 |
| 2 |
| 20 |
| 3×2 |
| 20 |
| 3×22 |
| 20 |
| 3×2n-1 |
| 20n-29 |
| 3×2n |
=-3+
| 20 |
| 3 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 20n-29 |
| 3×2n |
=-3+
| 20 |
| 3 |
| ||||
1-
|
| 20n-29 |
| 3×2n |
=
| 11 |
| 3 |
| 20 |
| 3•2n-1 |
| 20n-29 |
| 3×2n |
∴Tn=
| 22 |
| 3 |
| 20n+11 |
| 3×2n-1 |
| 22 |
| 3 |
∴满足Tn>9的n的集合为∅.
点评:本题考查数列的通项公式的求法,考查满足不等式的自然数的集合的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
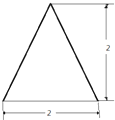 一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( )
一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( )A、4
| ||||
B、4
| ||||
C、4(
| ||||
| D、8,8 |
已知O是△ABC所在平面内一定点,动点P满足
=
+λ(
sinB+
sinC)(λ≥0),则P点的轨迹一定通过△ABC的( )
| OP |
| OA |
| AB |
| AC |
| A、内心 | B、外心 | C、垂心 | D、重心 |
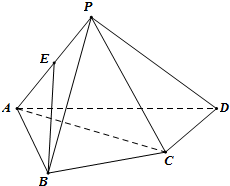 在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)
在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)