题目内容
下列命题中,真命题的序号是
①△ABC中,A>B?sinA>sinB
②数列{an}的前n项和Sn=n2-2n+1,则数列{an}是等差数列.
③锐角三角形的三边长分别为3,4,a,则a的取值范围是
<a<5.
④等差数列{an}前n项和为Sn,已知am-1+am+1-am2=0,S2m-1=38,则m=10.
①△ABC中,A>B?sinA>sinB
②数列{an}的前n项和Sn=n2-2n+1,则数列{an}是等差数列.
③锐角三角形的三边长分别为3,4,a,则a的取值范围是
| 7 |
④等差数列{an}前n项和为Sn,已知am-1+am+1-am2=0,S2m-1=38,则m=10.
考点:命题的真假判断与应用
专题:等差数列与等比数列,解三角形
分析:①,△ABC中,利用正弦定理,可判断①;
②,由数列{an}的前n项和Sn=n2-2n+1可求得an=
,从而可判断②;
③,利用锐角三角形的概念知32+a2>42,且32+42>a2,整理后可判断③;
④,利用等差数列的性质可求得am=0(舍)或am=2;再利用S2m-1=(2m-1)am=38,可求得m的值,从而可判断④.
②,由数列{an}的前n项和Sn=n2-2n+1可求得an=
|
③,利用锐角三角形的概念知32+a2>42,且32+42>a2,整理后可判断③;
④,利用等差数列的性质可求得am=0(舍)或am=2;再利用S2m-1=(2m-1)am=38,可求得m的值,从而可判断④.
解答:
解:对于①,△ABC中,A>B?a>b,由正弦定理知,a>b?sinA>sinB,所以△ABC中,A>B?sinA>sinB,即①正确;
对于②,数列{an}的前n项和Sn=n2-2n+1,
当n=1时,a1=S1=12-2×1+1=0,
当n≥2时,an=Sn-Sn-1=n2-2n-(n2-4n+3)=2n-3,
n=1时,a1=0不适合上式,
所以an=
,显然数列{an}不是等差数列,故②错误;
对于③,锐角三角形的三边长分别为3,4,a,
则32+a2>42,且32+42>a2,整理得:7<a2<25,
所以a的取值范围是
<a<5,故③正确;
对于④,等差数列{an}前n项和为Sn,由am-1+am+1-am2=0得:2am=am2,
所以,am=0或am=2;
由于S2m-1=(2m-1)am=38,
所以,am=2,2m-1=
=19,解得m=10,故④正确.
综上所述,真命题的序号是①③④.
故答案为:①③④.
对于②,数列{an}的前n项和Sn=n2-2n+1,
当n=1时,a1=S1=12-2×1+1=0,
当n≥2时,an=Sn-Sn-1=n2-2n-(n2-4n+3)=2n-3,
n=1时,a1=0不适合上式,
所以an=
|
对于③,锐角三角形的三边长分别为3,4,a,
则32+a2>42,且32+42>a2,整理得:7<a2<25,
所以a的取值范围是
| 7 |
对于④,等差数列{an}前n项和为Sn,由am-1+am+1-am2=0得:2am=am2,
所以,am=0或am=2;
由于S2m-1=(2m-1)am=38,
所以,am=2,2m-1=
| 38 |
| 2 |
综上所述,真命题的序号是①③④.
故答案为:①③④.
点评:本题考查命题的真假判断与应用,着重考查等差数列的判定与等差数列的性质的应用,考查正弦定理与三角形性形状的判定,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
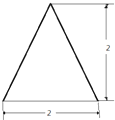 一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( )
一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( )A、4
| ||||
B、4
| ||||
C、4(
| ||||
| D、8,8 |
已知O是△ABC所在平面内一定点,动点P满足
=
+λ(
sinB+
sinC)(λ≥0),则P点的轨迹一定通过△ABC的( )
| OP |
| OA |
| AB |
| AC |
| A、内心 | B、外心 | C、垂心 | D、重心 |
 某中学某班对学生每天数学作业完成时间(分钟)进行调查,将所得数据调整后的频率分布表和频率分布直方图如图.
某中学某班对学生每天数学作业完成时间(分钟)进行调查,将所得数据调整后的频率分布表和频率分布直方图如图.