题目内容
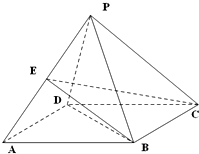 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=| 6 |
(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥E-ABC的体积.
考点:棱柱、棱锥、棱台的体积,棱锥的结构特征
专题:空间位置关系与距离
分析:(1)连接BD,AC交于O点,由已知得PO⊥BD,BD⊥AC,从而BD⊥面PAC,由此能证明BD⊥PC.
(2)由VE-ABC=VB-AEC,利用等积法能求出三棱锥E-ABC的体积.
(2)由VE-ABC=VB-AEC,利用等积法能求出三棱锥E-ABC的体积.
解答:
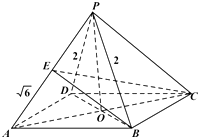 (1)证明:连接BD,AC交于O点,(1分)
(1)证明:连接BD,AC交于O点,(1分)
∵PB=PD,∴PO⊥BD,(2分)
又∵ABCD是菱形,∴BD⊥AC,(3分)
而AC∩PO=O,∴BD⊥面PAC,(5分)
∴BD⊥PC.(6分)
(2)解:由(1)知BD⊥面PAC,(7分)
S△AEC=
S△PAC=
×
×2
×sin45°=3,(9分)
∴VE-ABC=VB-AEC=
S△AEC•BO=
×3×
=
.(12分)
 (1)证明:连接BD,AC交于O点,(1分)
(1)证明:连接BD,AC交于O点,(1分)∵PB=PD,∴PO⊥BD,(2分)
又∵ABCD是菱形,∴BD⊥AC,(3分)
而AC∩PO=O,∴BD⊥面PAC,(5分)
∴BD⊥PC.(6分)
(2)解:由(1)知BD⊥面PAC,(7分)
S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 3 |
∴VE-ABC=VB-AEC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查异面直线垂直的证明,考查三棱锥的体积的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
已知集合A={x|x>1},B={x|x≥2},∁AB=( )
| A、[2,+∞) |
| B、(1,2] |
| C、(1,2) |
| D、(2,+∞) |
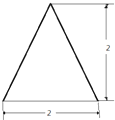 一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( )
一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( )A、4
| ||||
B、4
| ||||
C、4(
| ||||
| D、8,8 |
已知O是△ABC所在平面内一定点,动点P满足
=
+λ(
sinB+
sinC)(λ≥0),则P点的轨迹一定通过△ABC的( )
| OP |
| OA |
| AB |
| AC |
| A、内心 | B、外心 | C、垂心 | D、重心 |
已知a、b∈R,直线l1:ax+2y+3=0和直线l2:x+by+2=0,则“ab=2”是“l1∥l2”的( )
| A、充分不必要条件. |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件. |
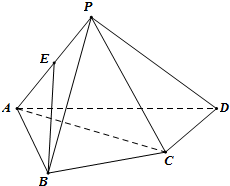 在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)
在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)