题目内容
已知:cotA+cotB+cotC=
,A+B+C=π.求证:A=B=C=
.
| 3 |
| π |
| 3 |
考点:三角函数恒等式的证明
专题:推理和证明
分析:依题意得cotA+cotB-
=
,令cotA+cotB=x,cotAcotB=y,可得y=x2-
x+1,cotA,cotB是t2-xt+x2-
x+1=0的两根,利用韦达定理及一元二次方程有根的条件,可求得△=0,从而可得A=B=
,得到结论.
| cotAcotB-1 |
| cotA+cotB |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
解答:
证明:因为cotA+cotB+cotC=cotA+cotB-cot(A+B)=cotA+cotB-
=
,
令cotA+cotB=x,cotAcotB=y,
则y=x2-
x+1,
cotA,cotB是t2-xt+x2-
x+1=0的两根,
所以又△=x2-4x2+4
x-4=-(
x-2)2≥0得:(
x-2)2≤0,又(
x-2)2≥0,
所以,(
x-2)2=0,解得:x=
,y=
,此时cotA=cotB,
即cotA=cotB=
,cotAcotB=
,
所以A=B=
,
所以,此三角形为正三角形,即A=B=C=
.
| cotAcotB-1 |
| cotA+cotB |
| 3 |
令cotA+cotB=x,cotAcotB=y,
则y=x2-
| 3 |
cotA,cotB是t2-xt+x2-
| 3 |
所以又△=x2-4x2+4
| 3 |
| 3 |
| 3 |
| 3 |
所以,(
| 3 |
2
| ||
| 3 |
| 1 |
| 3 |
即cotA=cotB=
| ||
| 3 |
| 1 |
| 3 |
所以A=B=
| π |
| 3 |
所以,此三角形为正三角形,即A=B=C=
| π |
| 3 |
点评:本题考查三角函数恒等式的证明,考查诱导公式与两角和的余切公式的应用,考查构造函数思想与韦达定理的应用,属于难题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知O是△ABC所在平面内一定点,动点P满足
=
+λ(
sinB+
sinC)(λ≥0),则P点的轨迹一定通过△ABC的( )
| OP |
| OA |
| AB |
| AC |
| A、内心 | B、外心 | C、垂心 | D、重心 |
 如图,在四棱锥P-ABCD中,底面ABCD是边长为
如图,在四棱锥P-ABCD中,底面ABCD是边长为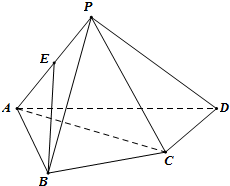 在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)
在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)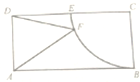 如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是
如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是
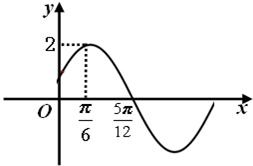 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<