题目内容
从长度为1、3、5、7、9个单位的五条线段中任取三条作边,能组成三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:分别列举出所有的基本事件,再找到满足条件的基本事件,利用古典概型的概率计算公式即可得出.
解答:
解:从长度分别为1,3,5,7,9个单位的5条线段中任取3条,分别为(1,3,5),(1,3,7),(1,3,9),(1,5,7),(1,5,9),(1,7,9),(3,5,7),(3,5,9),(3,7,9),(5,7,9)共有10种方法,其中能组成三角形的有以下3种:(3,5,7),(3,7,9),(5,7,9).
故能组成三角形的概率P=
,
故选:C.
故能组成三角形的概率P=
| 3 |
| 10 |
故选:C.
点评:本题考查了古典概型的概率计算公式、三个数能组成三角形的条件,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知O是△ABC所在平面内一定点,动点P满足
=
+λ(
sinB+
sinC)(λ≥0),则P点的轨迹一定通过△ABC的( )
| OP |
| OA |
| AB |
| AC |
| A、内心 | B、外心 | C、垂心 | D、重心 |
已知a、b∈R,直线l1:ax+2y+3=0和直线l2:x+by+2=0,则“ab=2”是“l1∥l2”的( )
| A、充分不必要条件. |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件. |
已知直线l1:(m-1)x+y+2=0,l2:8x+(m+1)y+(m-1)=0,则“m=3”是“l1∥l2”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
 某中学某班对学生每天数学作业完成时间(分钟)进行调查,将所得数据调整后的频率分布表和频率分布直方图如图.
某中学某班对学生每天数学作业完成时间(分钟)进行调查,将所得数据调整后的频率分布表和频率分布直方图如图.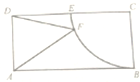 如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是
如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是