题目内容
7.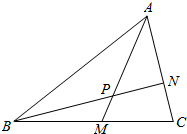 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 4 | D. | $\frac{5}{4}$ |
分析 M为BC中点,从而有$\overrightarrow{AM}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,这便可得到$\overrightarrow{AP}=\frac{λ}{2}\overrightarrow{AB}+\frac{λ}{2}\overrightarrow{AC}$,而B,P,N三点共线,并且AN=2NC,从而有$\overrightarrow{AP}=k\overrightarrow{AB}+\frac{2}{3}(1-k)\overrightarrow{AC}$,从而可得到$\left\{\begin{array}{l}{\frac{λ}{2}=k}\\{\frac{λ}{2}=\frac{2}{3}(1-k)}\end{array}\right.$,解出λ即可求出AP:PM的值.
解答 解:∵$\overrightarrow{AM}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,$\overrightarrow{AP}=λ\overrightarrow{AM}$;
∴$\overrightarrow{AP}=\frac{λ}{2}\overrightarrow{AB}+\frac{λ}{2}\overrightarrow{AC}$;
∵B,P,N三点共线;
∴$\overrightarrow{AP}=k\overrightarrow{AB}+(1-k)\overrightarrow{AN}$=$k\overrightarrow{AB}+\frac{2}{3}(1-k)\overrightarrow{AC}$;
∴$\left\{\begin{array}{l}{\frac{λ}{2}=k}\\{\frac{λ}{2}=\frac{2}{3}(1-k)}\end{array}\right.$;
解得$λ=\frac{4}{5}$;
∴AP:PM=4:1;
即AP:PM的值为4.
故选:C.
点评 考查向量加法的平行四边形法则,共线向量基本定理,以及平面向量基本定理,向量数乘的几何意义.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案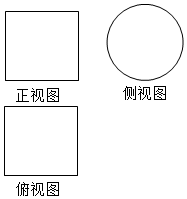 如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )| A. | 4π | B. | 6π | C. | 8π | D. | 16π |
| A. | ($\sqrt{3}$,3) | B. | (3,+∞) | C. | ($\sqrt{2}$,2) | D. | (2,+∞) |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 2x0<1<x0 | B. | x0<2x0<1 | C. | 1<x0<2x0 | D. | x0<1<2x0 |
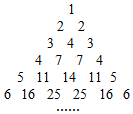 如图三角形数阵满足:
如图三角形数阵满足: