题目内容
17.已知点P(m,m)为角α终边上一点,m∈R,且m∈R,且m≠0,则sinα=±$\frac{\sqrt{2}}{2}$.分析 由题意可得x=m,y=m,r=$\sqrt{2}$m,由任意角的三角函数的定义,sinα=$\frac{y}{r}$,运算求得结果.
解答 解:由题意可得x=m,y=m,m∈R,且m≠0,
∴r=|$\sqrt{2}$m|,sinα=$\frac{y}{r}$=$\frac{m}{|\sqrt{2}m|}$=±$\frac{\sqrt{2}}{2}$,
故答案为:±$\frac{\sqrt{2}}{2}$.
点评 本题主要考查任意角的三角函数的定义,两点间的距离公式的应用,属于基础题.

练习册系列答案
相关题目
7.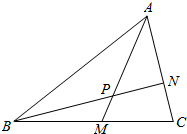 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 4 | D. | $\frac{5}{4}$ |
8.已知$\overrightarrow{a}$=(m-2,m+3),$\overrightarrow{b}$=(2m+1,m-2),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是锐角,则实数m的取值范围是( )
| A. | m>2或m<-$\frac{4}{3}$ | B. | -$\frac{4}{3}$<m<2 | C. | m≠2 | D. | m≠2且m≠-$\frac{4}{3}$ |
12.已知cosα=$\frac{\sqrt{5}}{7}$,且sinα<0,则角α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
9.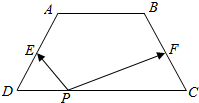 如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )
如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )
 如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )
如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )| A. | (-$\frac{5}{4}$,-$\frac{9}{20}$) | B. | (-$\frac{9}{20}$,$\frac{11}{4}$) | C. | (-$\frac{9}{20}$,-$\frac{1}{4}$) | D. | (-$\frac{5}{4}$,$\frac{11}{4}$) |
6.已知常数a>$\frac{1}{2}$,则函数y=x2+|x-a|+1的最小值为( )
| A. | a+1 | B. | a+$\frac{3}{4}$ | C. | a2+1 | D. | $\frac{3}{4}$-a |