题目内容
12.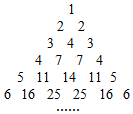 如图三角形数阵满足:
如图三角形数阵满足:(1)第n行首尾两数均为n;
(2)图中的递推关系类似于杨辉三角.
则第n(n≥2)行第2个数是$\frac{{n}^{2}-n+2}{2}$,第n行的和是2n+2n-1-2.
分析 计算前5行的第二个数字与前5行的数字和,发现其中的规律,得出结论.
解答 解:设第n行的第2个数为an,由图可知,a2=2=1+1,a3=4=1+2+1,a4=7=1+2+3+1,a5=11=1+2+3+4+1…
归纳可得an=1+2+3+4+…+(n-1)+1=$\frac{n(n-1)}{2}+1$=$\frac{{n}^{2}-n+2}{2}$.
设第n行的和为Sn,则S2=4=22,S3=10=2S2+2=23+2,S4=22=2S3+2=24+22+2.S5=46=2S4+2=25+23+22+2…
归纳可得Sn=2n+2n-2+2n-3+…+23+22+2=2n+$\frac{2(1-{2}^{n-2})}{1-2}$=2n+2n-1-2.
故答案为$\frac{{n}^{2}-n+2}{2}$,2n+2n-1-2.
点评 本题考查了归纳推理,等差数列,等比数列求和,属于基础题.

练习册系列答案
相关题目
2.设f(x)是定义域为R且最小正周期为2π的函数,且有f(x)=$\left\{\begin{array}{l}{sinx,0≤x≤π}\\{cosx,-π<x<0}\end{array}\right.$,则f(-$\frac{13π}{4}$)=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | 0 | D. | 1 |
20.在如下程序框图中,已知f0(x)=sinx,则输出的结果是( )


| A. | sinx | B. | cosx | C. | -sinx | D. | -cosx |
7.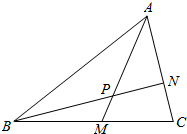 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 4 | D. | $\frac{5}{4}$ |
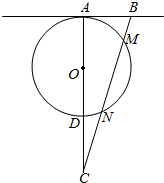 如图所示,AD是⊙O的直径,AB是⊙O的切线,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,求CD的长和⊙O的半径.
如图所示,AD是⊙O的直径,AB是⊙O的切线,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,求CD的长和⊙O的半径.