题目内容
17.已知p:(x-m+1)(x-m-1)<0;q:$\frac{1}{2}$<x<$\frac{2}{3}$,若p是q的必要不充分条件,则实数m的取值范围是$[-\frac{1}{3},\frac{3}{2}]$.分析 求出p的等价条件,利用必要不充分条件的定义建立不等式关系进行求解即可.
解答 解:p的等价条件是m-1<x<m+1,
若p是q的必要不充分条件,
则$\left\{\begin{array}{l}{m+1≥\frac{2}{3}}\\{m-1≤\frac{1}{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{m≥-\frac{1}{3}}\\{m≤\frac{3}{2}}\end{array}\right.$,即$-\frac{1}{3}$≤m≤$\frac{3}{2}$,
故答案为:$[-\frac{1}{3},\frac{3}{2}]$.
点评 本题主要考查充分条件和必要条件的应用,根据充分条件和必要条件建立不等式关系是解决本题的关键.比较基础.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
7.已知a=log32,b=(log32)2,c=log4$\frac{2}{3}$,则( )
| A. | a<c<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
8.若曲线f(x)=x3+x-2在点P0处的切线垂直于直线x+4y+3=0,则点P0的坐标为( )
| A. | (1,0) | B. | (2,8) | C. | (2,8)或(-1,-4) | D. | (1,0)或(-1,-4) |
12.已知|${\overrightarrow a}$|=1,|${\overrightarrow b$|=2$\sqrt{3}$,$\overrightarrow a$•(${\overrightarrow b$-$\overrightarrow a}$)=-4,则向量$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
2.设f(x)是定义域为R且最小正周期为2π的函数,且有f(x)=$\left\{\begin{array}{l}{sinx,0≤x≤π}\\{cosx,-π<x<0}\end{array}\right.$,则f(-$\frac{13π}{4}$)=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | 0 | D. | 1 |
7.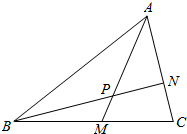 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 4 | D. | $\frac{5}{4}$ |
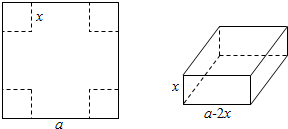 有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?
有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?