题目内容
16.已知x0是函数f(x)=2x-log0.5x的零点.则( )| A. | 2x0<1<x0 | B. | x0<2x0<1 | C. | 1<x0<2x0 | D. | x0<1<2x0 |
分析 先判断函数ff(x)=2x-log0.5x的零点所在区间,我们可以利用零点存在定理,即函数f(x)在区间(a,b)上若f(a)•(b)<0,则函数f(x)在区间(a,b)上有零点,再根据指数函数的性质即可判断.
解答 解:∵f(x)=2x-log0.5x在其定义域为单调增函数,
f($\frac{1}{2}$)=$,\sqrt{2}$-1>0,f($\frac{1}{4}$)=${2}^{\frac{1}{4}}$-log0.5$\frac{1}{4}$=${2}^{\frac{1}{4}}$-2<0,
∴f($\frac{1}{4}$)f($\frac{1}{2}$)<0,
∴函数f(x)零点在($\frac{1}{4}$,$\frac{1}{2}$)上,
即x0∈($\frac{1}{4}$,$\frac{1}{2}$),
∴2x0>1,
∴x0<1<2x0
故选:D.
点评 本题考查的知识点是根的存在性及根的个数判断,牢固掌握零点存在定理,即函数f(x)在区间(a,b)上若f(a)•(b)<0,则函数f(x)在区间(a,b)上有零点,是解答本题的关键.

练习册系列答案
相关题目
7.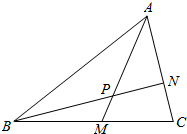 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 4 | D. | $\frac{5}{4}$ |
8.已知$\overrightarrow{a}$=(m-2,m+3),$\overrightarrow{b}$=(2m+1,m-2),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是锐角,则实数m的取值范围是( )
| A. | m>2或m<-$\frac{4}{3}$ | B. | -$\frac{4}{3}$<m<2 | C. | m≠2 | D. | m≠2且m≠-$\frac{4}{3}$ |
6.已知常数a>$\frac{1}{2}$,则函数y=x2+|x-a|+1的最小值为( )
| A. | a+1 | B. | a+$\frac{3}{4}$ | C. | a2+1 | D. | $\frac{3}{4}$-a |