题目内容
19.设{an}是无穷数列,令a′k=$\frac{{a}_{k}+{a}_{k+1}}{2}$,(k=1,2,…),则称{a′k}是{ak}的均值数列.仿此可定义,{a″k}是{a′k}的均值数列,且{a″k}是{a′k}的第二级均值数列.若{ak}的各级均值数列都是整数列,则称{ak}是“好”数列,求证:若{ak}是“好”数列,则{ak2}也是“好”数列.分析 由新定义可得,{ak}的各级均值数列都是整数列,即有{ak}均为奇数构成的数列或均为偶数构成的数列,根据奇数的平方必为奇数,偶数的平方必为偶数,即可得证.
解答 证明:若{ak}是“好”数列,
由新定义可得,{ak}的各级均值数列都是整数列,
即有{ak}均为奇数构成的数列或均为偶数构成的数列,
根据奇数的平方必为奇数,偶数的平方必为偶数,
可得{ak2}的各级均值数列都是整数列,
由新定义可得{ak2}也是“好”数列.
点评 本题考查新定义的理解和运用,注意运用奇数和偶数的性质是解题的关键,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.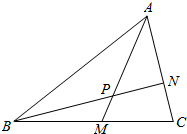 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
 如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )
如图,在△ABC中,点M是BC中点,点N在AC上,且AN=2NC,AM交BN于点P,则AP:PM的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 4 | D. | $\frac{5}{4}$ |
8.已知$\overrightarrow{a}$=(m-2,m+3),$\overrightarrow{b}$=(2m+1,m-2),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是锐角,则实数m的取值范围是( )
| A. | m>2或m<-$\frac{4}{3}$ | B. | -$\frac{4}{3}$<m<2 | C. | m≠2 | D. | m≠2且m≠-$\frac{4}{3}$ |
9.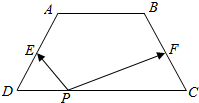 如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )
如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )
 如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )
如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )| A. | (-$\frac{5}{4}$,-$\frac{9}{20}$) | B. | (-$\frac{9}{20}$,$\frac{11}{4}$) | C. | (-$\frac{9}{20}$,-$\frac{1}{4}$) | D. | (-$\frac{5}{4}$,$\frac{11}{4}$) |
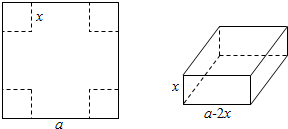 有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?
有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?