题目内容
10.已知函数f(x)=lnx+$\frac{a}{x}$(a>0).(Ⅰ)求函数f(x)在[1,+∞)上的最小值;
(Ⅱ)若存在三个不同的实数xi(i=1,2,3)满足f(x)=ax.
(i)证明:?a∈(0,1),f($\frac{{a}^{2}}{2}$)>$\frac{{a}^{3}}{2}$;
(ii)求实数a的取值范围及x1•x2•x3的值.
分析 (Ⅰ)求出f(x)的导数,对a讨论,当a≥1时,当0<a<1时,讨论单调区间,可得最小值;
(Ⅱ)(i)求出f($\frac{{a}^{2}}{2}$)-$\frac{{a}^{3}}{2}$,构造函数g(a)=2lna-$\frac{{a}^{3}}{2}$+$\frac{2}{a}$-ln2,利用导数求得g(a)>g(1)=2-$\frac{1}{2}$-ln2>0,问题得以证明;
(ii)求出原函数的导函数,然后讨论0<a<$\frac{1}{2}$f(x)的零点的个数,即可得到x1•x2•x3的值.
解答 解:(Ⅰ)函数f(x)的导数为f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,
当a≥1时,f(x)在[1,a]递减,在[a,+∞)递增,
可得f(x)在x=a取得极小值,且为最小值lna+1;
当0<a<1时,f′(x)>0,f(x)在[1,+∞)递增,
f(1)取得最小值,且为a.
综上可得当a≥1时,f(x)的最小值为lna+1;
当0<a<1时,f(x)的最小值为a;
(Ⅱ)(i)证明:∵f(x)-ax=lnx-ax+$\frac{a}{x}$,
∴f($\frac{{a}^{2}}{2}$)-$\frac{{a}^{3}}{2}$=ln$\frac{{a}^{2}}{2}$-$\frac{{a}^{3}}{2}$+$\frac{2}{a}$=2lna-$\frac{{a}^{3}}{2}$+$\frac{2}{a}$-ln2,
令g(a)=2lna-$\frac{{a}^{3}}{2}$+$\frac{2}{a}$-ln2,
∴g′(a)=$\frac{2}{a}$-$\frac{2}{{a}^{2}}$-$\frac{3{a}^{2}}{2}$=$\frac{-3{a}^{4}+4(a-1)}{2{a}^{2}}$,
∴a∈(0,1)时,g'(a)<0,g(a)单调递减,
∴g(a)>g(1)=2-$\frac{1}{2}$-ln2>0,
∴?a∈(0,1),f($\frac{{a}^{2}}{2}$)>$\frac{{a}^{3}}{2}$;
(ii)∵f(x)-ax的导数为f′(x)-a=$\frac{1}{x}$-a(1+$\frac{1}{{x}^{2}}$)=$\frac{-a{x}^{2}+x-a}{{x}^{2}}$,
令f′(x)=a,∴-ax2+x-a=0,
∵函数f(x)-ax存在不同的零点,∴△=1-4a2>0,
解得-$\frac{1}{2}$<a<$\frac{1}{2}$,
由0<a<$\frac{1}{2}$,令f′(x)=a,得,x4=$\frac{1-\sqrt{1-4{a}^{2}}}{2a}$,x5=$\frac{1+\sqrt{1-4{a}^{2}}}{2a}$,
此时,f(x)在(0,x4)上递减,(x4,x5)上递增,(x5,+∞)上递减,
∴f(x)至多有三个零点.
∵f(x)在(x4,1)递增,∴f(x4)<f(1)=a,
又∵f($\frac{{a}^{2}}{2}$)>$\frac{{a}^{3}}{2}$,
∴?x0∈($\frac{{a}^{2}}{2}$,x4),使得f(x0)=a,
又f( $\frac{1}{{x}_{0}}$)=-f(x0)=a,f(1)=a,
∴恰有三个不同零点:x0,1,$\frac{1}{{x}_{0}}$,
∴函数f(x)存在三个不同的零点时,a的取值范围是(0,$\frac{1}{2}$);
且x1•x2•x3的值为1.
点评 本题主要考查基本初等函数的导数、导数的运算及导数的应用;考查推理论证能力、运算求解能力以及应用意识,考查化归与转化思想、分类与整合思想、函数与方程思想,属于难题.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案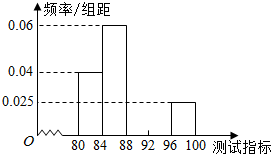 某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:| 组号 | 测试指标 | 频数 | 频率 |
| 第一组 | [80,84] | 8 | 0.16 |
| 第二组 | [84,88] | x | 0.24 |
| 第三组 | [88,92] | 15 | p |
| 第四组 | [92,96] | 10 | q |
| 第五组 | [96,100] | y | 0.1 |
| 合 计 | 50 | 1 | |
(2)为了挑选最优质的芯片,工厂决定在第三、四、五组中用分层抽样法抽取6件产品进行第二次检测,最终决定选用2件产品,求2件产品中至少有1件来自第四组的概率.
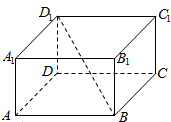 如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.
如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.