题目内容
从大量面值为一元和五元的纸币中取出若干张，使总值为100元，求：
（1）共有多少种取法？
（2）每种取法中各种面值的纸币各为多少张？
（3）画出算法的程序框图．
（1）共有多少种取法？
（2）每种取法中各种面值的纸币各为多少张？
（3）画出算法的程序框图．
考点：设计程序框图解决实际问题,列举法计算基本事件数及事件发生的概率
专题：算法和程序框图
分析：（1）设x和y分别表示一元和五元的纸币张数，有x+5y=100，共有21种取法．
（2）由x+5y=100，y的取值范围为[0，20]上的整数，把满足条件的x，y列表写出即可．
（3）由（1）（2）可确定算法画出程序框图．
（2）由x+5y=100，y的取值范围为[0，20]上的整数，把满足条件的x，y列表写出即可．
（3）由（1）（2）可确定算法画出程序框图．
解答：
解：（1）设x和y分别表示一元和五元的纸币张数，显然有x+5y=100，y的取值范围为[0，20]上的整数，故共有21种取法．
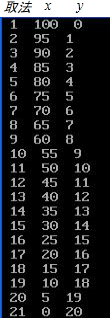
（2）每种取法中各种面值的纸币数如下表（x和y分别表示一元和五元的纸币张数）：
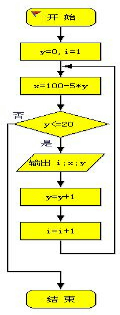
（3）算法的程序框图如下：
（2）每种取法中各种面值的纸币数如下表（x和y分别表示一元和五元的纸币张数）：
（3）算法的程序框图如下：
点评：本题主要考察设计程序框图解决实际问题，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
若函数f（x）=
在R上为增函数，则a的取值范围是（ ）
|
| A、（1，2] |
| B、（1，+∞） |
| C、[1，+∞） |
| D、（1，2） |
已知数列{an}满足a1=0，an+1=an+2n，那么a2015的值是（ ）
| A、2 012×2 013 |
| B、2 014×2 015 |
| C、2 0142 |
| D、2 013×2 014 |
下列函数中，在区间（0，1）上是递增函数的是（ ）
| A、y=|x+1| | ||
| B、y=3-x | ||
C、y=
| ||
| D、y=-x2+4 |
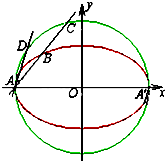如图，已知椭圆E1：