题目内容
已知等腰△ABC的顶点A（-1，2），直线AC的斜率为
，点B（-3，2），求直线AC，BC及∠A的平分线所在的方程．
| 3 |
考点：两直线的夹角与到角问题
专题：分类讨论,直线与圆
分析：根据题目条件求出AC的方程，由A，B点求出AB方程，直线AC的斜率为
，求出倾斜角60°，再分类求出BC的倾斜角，求BC时运用其倾斜角求解斜率．
| 3 |
解答：
解：∵等腰△ABC的顶点A（-1，2），直线AC的斜率为
，
∴AC：y=
x+2+
，
∵A（-1，2），点B（-3，2），
∴AB∥x轴，AC的倾斜角为60，
可得BC倾斜角为30°或120°．
当α=30°时，BC方程为y=
x+2+
，
∵角A平分线倾斜角为120°，∴所在直线方程为y=-
x+2-
，
当α=120°时，BC方程为y=-
x+2-3
，
角A平分线倾斜角为30，
∴所在直线方程为y=
x+2+
，
| 3 |
∴AC：y=
| 3 |
| 3 |
∵A（-1，2），点B（-3，2），
∴AB∥x轴，AC的倾斜角为60，
可得BC倾斜角为30°或120°．
当α=30°时，BC方程为y=
| ||
| 3 |
| 3 |
∵角A平分线倾斜角为120°，∴所在直线方程为y=-
| 3 |
| 3 |
当α=120°时，BC方程为y=-
| 3 |
| 3 |
角A平分线倾斜角为30，
∴所在直线方程为y=
| ||
| 3 |
| ||
| 3 |
点评：本题综合考查了直线的方程，位置关系的知识，整个解题过程运用倾斜角，点的坐标求解方程．
练习册系列答案
相关题目
已知数列{an}满足a1=0，an+1=an+2n，那么a2015的值是（ ）
| A、2 012×2 013 |
| B、2 014×2 015 |
| C、2 0142 |
| D、2 013×2 014 |
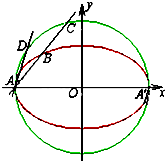如图，已知椭圆E1：