题目内容
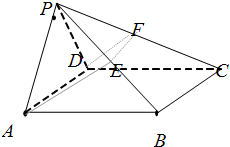 四棱锥P-ABCD中,底面ABCD是∠DAB=60°的菱形,侧面PAD为正三角形.
四棱锥P-ABCD中,底面ABCD是∠DAB=60°的菱形,侧面PAD为正三角形.(1)AD⊥PB;
(2)若E为PB边的中点,过三点A、D、E的平面交PC于点F,证明:F为PC的中点.
考点:棱锥的结构特征,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)取AD的中点M,连PM,BM,只要证明AD⊥平面PBM即可;
(2)充分利用底面是菱形以及E为PB边的中点,利用线面平行的判定和性质,只要得到EF∥BC即可.
(2)充分利用底面是菱形以及E为PB边的中点,利用线面平行的判定和性质,只要得到EF∥BC即可.
解答:
证明:(1)取AD的中点M,连PM,BM,则∵侧面PAD为正三角形,
∴PM⊥AD,
又底面ABCD是∠DAB=60°的菱形,
∴三角形ABD是等边三角形,
∴AD⊥BM,
∴AD⊥平面PBM,
∴AD⊥PB(7分);
(2)∵底面ABCD是菱形,
∴AD∥BC,又AD?平面PBC,BC?平面PBC,
∴AD∥平面PBC,
AD?平面ADFE,平面ADFE∩平面PBC=EF,
∴AD∥EF,
∵AD∥BC.
∴BC∥EF,
又E为PB的中点,故F为PC的中点. (14分)
∴PM⊥AD,
又底面ABCD是∠DAB=60°的菱形,
∴三角形ABD是等边三角形,
∴AD⊥BM,
∴AD⊥平面PBM,
∴AD⊥PB(7分);
(2)∵底面ABCD是菱形,
∴AD∥BC,又AD?平面PBC,BC?平面PBC,
∴AD∥平面PBC,
AD?平面ADFE,平面ADFE∩平面PBC=EF,
∴AD∥EF,
∵AD∥BC.
∴BC∥EF,
又E为PB的中点,故F为PC的中点. (14分)
点评:本题考查了几何体棱锥中的线面关系;考查了线面平行的判定和性质的运用;熟练掌握线面平行的判定定理和性质定理是解答问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
复数(
)2013(i为虚数单位)等于( )
| 1+i |
| 1-i |
| A、i | B、-i | C、1 | D、-1 |
下列函数中,在区间(0,1)上是递增函数的是( )
| A、y=|x+1| | ||
| B、y=3-x | ||
C、y=
| ||
| D、y=-x2+4 |
已知O为坐标原点,A(1,2),点P(x,y)满足约束条件
,则Z=
•
的最大值为( )
|
| OA |
| OP |
| A、-2 | B、-1 | C、1 | D、2 |
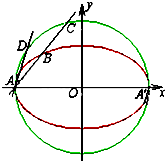 如图,已知椭圆E1:
如图,已知椭圆E1: