题目内容
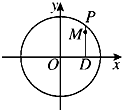 如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为PD上一点,且|PD|=
如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为PD上一点,且|PD|=| 2 |
(Ⅰ)求证:曲线C是焦点在x轴上的椭圆,并求其方程;
(Ⅱ)设椭圆C的右焦点为F2,直线l:y=kx+m与椭圆C交于A、B两点,直线F2A与F2B的倾斜角互补,求证:直线l过定点,并求该定点的坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设M的坐标为(x,y),P的坐标为(xP,yP),由已知得
,由此能证明曲线C是焦点在x轴上的椭圆,并能求出其方程.
(Ⅱ)设直线AB方程为y=kx+m,由
,得(2k2+1)x2+4kmx+2m2-2=0,由此利用韦达定理结合已知条件能证明直线MN过定点(2,0).
|
(Ⅱ)设直线AB方程为y=kx+m,由
|
解答:
(Ⅰ)证明:设M的坐标为(x,y),P的坐标为(xP,yP),
由已知得
,
∵P在圆上,∴x2+(
y)2=2,即
+y2=1,
∴曲线C是焦点在x轴上的椭圆,其方程为
+y2=1.
(Ⅱ)证明:由题意,知直线AB斜率存在,其方程为y=kx+m,
由
,消去y,得(2k2+1)x2+4kmx+2m2-2=0,
△=(4km)2-4(2k2+1)(2m2-2)>0.
设A(x1,y1),B(x2,y2),
则x1+x2=-
,x1x2=
,
且kF2A=
,kF2B=
,
由已知直线F2A与F2B的倾斜角互补得,
kF2M+kF2N=0,即
+
=0,
化简得,2kx1x2+(m-k)(x1+x2)-2m=0,
∴2k•
-
-2m=0,
整理得,m=-2k,
∴直线MN的方程为y=k(x-2),
故直线MN过定点,该定点的坐标为(2,0).
由已知得
|
∵P在圆上,∴x2+(
| 2 |
| x2 |
| 2 |
∴曲线C是焦点在x轴上的椭圆,其方程为
| x2 |
| 2 |
(Ⅱ)证明:由题意,知直线AB斜率存在,其方程为y=kx+m,
由
|
△=(4km)2-4(2k2+1)(2m2-2)>0.
设A(x1,y1),B(x2,y2),
则x1+x2=-
| 4km |
| 2k2+1 |
| 2m2-2 |
| 2k2+1 |
且kF2A=
| kx1+m |
| x1-1 |
| kx2+m |
| x2-1 |
由已知直线F2A与F2B的倾斜角互补得,
kF2M+kF2N=0,即
| kx1+m |
| x1-1 |
| kx2+m |
| x2-1 |
化简得,2kx1x2+(m-k)(x1+x2)-2m=0,
∴2k•
| 2m2-2 |
| 2k2+1 |
| 4km(m-k) |
| 2k2+1 |
整理得,m=-2k,
∴直线MN的方程为y=k(x-2),
故直线MN过定点,该定点的坐标为(2,0).
点评:本题考查曲线是椭圆的证明,考查直线过定点的证明,解题时要认真审题,熟练掌握椭圆的简单性质及其应用.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
设a∈R,i是虚数单位,则“a=1”是“
为纯虚数”的( )
| a+i |
| a-i |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |