题目内容
已知奇函数f（x）在（0，+∞）上为减函数，且f（3）=0，求f（x）＞0的解集．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：首先，得到函数在（-∞，0）上为减函数，然后，得到f（-3）=0，最后，结合奇函数的图象关于坐标原点对称，从而确定不等式的解集．
解答：
解：∵奇函数f（x）在（0，+∞）上为减函数，
∴函数在（-∞，0）上为减函数，
∵f（3）=0，
∴f（-3）=0，
∵函数f（x）在（0，+∞）上为减函数，
∴当0＜x＜3时，f（x）＞0，
∵函数的图象关于坐标原点对称，
∴当x＜-3时，f（x）＞0，
综上，当x＜-3或0＜x＜3时，f（x）＞0，
∴f（x）＞0的解集{x|x＜-3或0＜x＜3}．
∴函数在（-∞，0）上为减函数，
∵f（3）=0，
∴f（-3）=0，
∵函数f（x）在（0，+∞）上为减函数，
∴当0＜x＜3时，f（x）＞0，
∵函数的图象关于坐标原点对称，
∴当x＜-3时，f（x）＞0，
综上，当x＜-3或0＜x＜3时，f（x）＞0，
∴f（x）＞0的解集{x|x＜-3或0＜x＜3}．
点评：本题重点考查了函数的单调性和奇偶性，及其运用，注意奇函数的图象特征，属于中档题．
练习册系列答案
相关题目
一个几何体的三个视图都是矩形，则该几何体可以是（ ）
| A、棱柱 | B、棱台 | C、圆柱 | D、棱锥 |
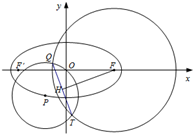在平面直角坐标系xOy中，已知椭圆
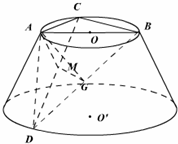如图所示，AB是圆台上底面⊙O的直径，C是⊙O上不同于A、B的一点，D是圆台下底面⊙O′上的一点，过A、B、C、D的截面垂直与底面，M是CD的中点，又AC=AD=2，∠CAD=120°，∠BCD=30°．
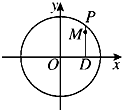如图，设P是圆x2+y2=2上的动点，点D是P在x轴上的投影，M为PD上一点，且|PD|=