题目内容
已知函数f(x)=cos2x
(1)设函数g(x)=f(x)+f(x-
),求函数g(x)的单调递增区间;
(2)函数h(x)=f(x)-asinx在x∈R上有最小值为-1,求a的值;
(3)当θ∈[0,
]时,关于θ的方程f(θ)-2mf(
)+4m-3=0有解,求实数m的取值范围.
(1)设函数g(x)=f(x)+f(x-
| π |
| 4 |
(2)函数h(x)=f(x)-asinx在x∈R上有最小值为-1,求a的值;
(3)当θ∈[0,
| π |
| 2 |
| θ |
| 2 |
考点:三角函数中的恒等变换应用,余弦定理的应用
专题:三角函数的求值,三角函数的图像与性质
分析:(1)对函数g(x)的解析式利用二倍角公式化简整理,利用三角函数的性质求得g(x)的单调递增区间;
(2)求出h(x)的解析式,利用换元法,转化为一元二次函数,分类讨论确定a的值.
(3)整理方程,利用换元法转化为一元二次方程,利用数形结合思想,利用抛物线的性质求得答案.
(2)求出h(x)的解析式,利用换元法,转化为一元二次函数,分类讨论确定a的值.
(3)整理方程,利用换元法转化为一元二次方程,利用数形结合思想,利用抛物线的性质求得答案.
解答:
解:(1)g(x)=f(x)+f(x-
)=cos2x+cos(2x-
)=cos2x+sin2x=
sin(2x+
)
∴当2kπ-
≤2x+
≤2kπ+
(k∈Z),即kπ-
≤x≤kπ+
(k∈Z)时,函数g(x)单调递增,
∴g(x)单调递增区间为[kπ-
,kπ+
](k∈Z).
(2)h(x)=f(x)-asinx=cos2x-asinx=1-2sin2x-asinx,
令sinx=t,则-1≤t≤1,
h(t)=-2t2-at+1,函数为开口向下,对称轴为t=-
的抛物线,
当-
≤-1时,即a≥4时,函数在[-1,1]上单调减,h(t)min=h(1)=-2-a+1=-1,求得a=0,与a≥4矛盾舍去.
当-
≥1时,即a≤-4,函数在[-1,1]上单调增,h(t)min=h(-1)=-2+a+1=-1,求得a=0,与a≤-4矛盾舍去
当0≥-
≥-1时,即0≤a≤4,h(t)min=h(1)=-2-a+1=-1,求得a=0
当1≥-
≥0时,即-4≤a≤0时,h(t)min=h(-1)=-2+a+1=-1,求得a=0,
综合可知a=0.
(3)f(θ)-2mf(
)+4m-3=cos2θ-2mcosθ+4m-3=2cos2θ-2mcosθ+4m-2=0,
令cosθ=t,则-1≤t≤1则2t2-2mt+4m-2=0,在[-1,1]有实数解,
即函数f(t)=2t2-2mt+4m-2的图象与x轴有交点,
①当有一个交点时,需
或
或
解得m的范围为∅,
②当有两个交点时,需
,解得0<m<4-2
| π |
| 4 |
| π |
| 2 |
| 2 |
| π |
| 4 |
∴当2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
∴g(x)单调递增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
(2)h(x)=f(x)-asinx=cos2x-asinx=1-2sin2x-asinx,
令sinx=t,则-1≤t≤1,
h(t)=-2t2-at+1,函数为开口向下,对称轴为t=-
| a |
| 4 |
当-
| a |
| 4 |
当-
| a |
| 4 |
当0≥-
| a |
| 4 |
当1≥-
| a |
| 4 |
综合可知a=0.
(3)f(θ)-2mf(
| θ |
| 2 |
令cosθ=t,则-1≤t≤1则2t2-2mt+4m-2=0,在[-1,1]有实数解,
即函数f(t)=2t2-2mt+4m-2的图象与x轴有交点,
①当有一个交点时,需
|
|
|
解得m的范围为∅,
②当有两个交点时,需
|
| 3 |
点评:本题主要考查了三角函数的恒等变换,换元法思想,一元二次函数的图象和性质等问题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
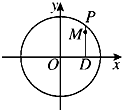 如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为PD上一点,且|PD|=
如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为PD上一点,且|PD|= 如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.
如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.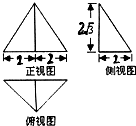 一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为
一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为