题目内容
某市规定,高中学生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
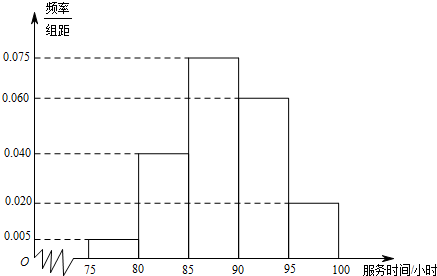
(Ⅰ)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(Ⅱ)从全市高中学生(人数很多)中任意选取3位学生,记ξ为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量ξ的分布列和数学期望Eξ.

(Ⅰ)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(Ⅱ)从全市高中学生(人数很多)中任意选取3位学生,记ξ为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量ξ的分布列和数学期望Eξ.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:应用题,概率与统计
分析:(Ⅰ)利用频率分布直方图,求出频率,即可求得结论;
(Ⅱ)ξ=0,1,2,3,求出随机变量取每一个值的概率值,即可求随机变量ξ的分布列及数学期望.
(Ⅱ)ξ=0,1,2,3,求出随机变量取每一个值的概率值,即可求随机变量ξ的分布列及数学期望.
解答:
解:(Ⅰ)抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为(0.06+0.02)×5×200=80人
参加社区服务时间不少于90小时的概率
=0.4;
(Ⅱ)ξ=0,1,2,3,则
P(ξ=0)=0.63=0.216,P(ξ=1)=
•0.4•0.62=0.432,P(ξ=2)=
•0.42•0.6=0.288,P(ξ=3)=0.43=0.064
∴ξ的分布列为
数学期望Eξ=1×0.432+2×0.288+3×0.064=1.2.
参加社区服务时间不少于90小时的概率
| 80 |
| 200 |
(Ⅱ)ξ=0,1,2,3,则
P(ξ=0)=0.63=0.216,P(ξ=1)=
| C | 1 3 |
| C | 2 3 |
∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | 0.216 | 0.432 | 0.288 | 0.064 |
点评:求随机变量的分布列与期望的关键是确定变量的取值,求出随机变量取每一个值的概率值.

练习册系列答案
相关题目
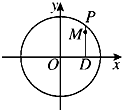 如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为PD上一点,且|PD|=
如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为PD上一点,且|PD|= 如图是某校校门的一个局部的截面设计图,CA=AO=OB=2米,
如图是某校校门的一个局部的截面设计图,CA=AO=OB=2米,
 如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.
如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.