题目内容
设a∈R，i是虚数单位，则“a=1”是“
为纯虚数”的（ ）
| a+i |
| a-i |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据纯虚数实数为0，虚部不为0，结合充要条件的定义，判断“a=1”与“
为纯虚数”的充要关系，可得答案．
| a+i |
| a-i |
解答：
解：∵
=
，
∴“
为纯虚数”?“a=±1”，
故“a=1”是“
为纯虚数”的充分不必要条件，
故选：A．
| a+i |
| a-i |
| a2-1+2ai |
| a2+1 |
∴“
| a+i |
| a-i |
故“a=1”是“
| a+i |
| a-i |
故选：A．
点评：本题考查的知识点是充要条件，熟练掌握充要条件的定义是解答的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
复数a十bi（a，b∈R）的平方为实数的充要条件是（ ）
| A、a2+b2=0 |
| B、ab=0 |
| C、a=0，且b≠0 |
| D、a≠0，且b=0 |
一个几何体的三个视图都是矩形，则该几何体可以是（ ）
| A、棱柱 | B、棱台 | C、圆柱 | D、棱锥 |
若实数x、y满足条件
，则z=x+3y的最大值为（ ）
|
| A、9 | B、11 | C、12 | D、16 |
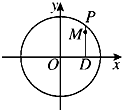如图，设P是圆x2+y2=2上的动点，点D是P在x轴上的投影，M为PD上一点，且|PD|=