题目内容

当圆x2+y2=4的圆心到直线y=kx+1的距离最大时，k=
 
．
考点：圆的切线方程
专题：计算题,直线与圆
分析：确定圆x2+y2=4的圆心C（0，0），直线y=kx+1恒过定点B（0，1），利用当直线与BC垂直时，圆心C到直线y=kx+1的距离最大，即可得出结论．
解答： 解：圆x2+y2=4的圆心C（0，0），直线y=kx+1恒过定点B（0，1），
当直线与BC垂直时，圆心C到直线y=kx+1的距离最大，
∵BC的斜率不存在，
∴垂直关系可得k=0，
故答案为：0．
点评：本题考查点到直线的距离和直线与圆的位置关系，属基础题．
练习册系列答案
相关题目
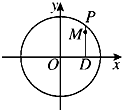如图，设P是圆x2+y2=2上的动点，点D是P在x轴上的投影，M为PD上一点，且|PD|=
2
|MD|，当P在圆上运动时，记点M的轨迹为曲线C．
（Ⅰ）求证：曲线C是焦点在x轴上的椭圆，并求其方程；
（Ⅱ）设椭圆C的右焦点为F2，直线l：y=kx+m与椭圆C交于A、B两点，直线F2A与F2B的倾斜角互补，求证：直线l过定点，并求该定点的坐标．
已知函数f（x）由下表定义：
x 1 2 3 4 5
f（x） 4 1 3 5 2
若a1=5，an+1=f（an）（n=1，2，…），则a2014=
 
．
设m为不小于2的正整数，对任意n∈Z，若n=qm+r（其中q，r∈Z，且0≤r≤m），则记fm（n）=r，如f2（3）=1，f3（8）=2．下列关于该映射fm：Z→Z的命题中，正确的是
 
．
①若a，b∈Z，则fm（a+b）=fm（a）+fm（b）
②若a，b，k∈Z，且fm（a）=m（b），则fm（ka）=fm（kb）
③若a，b，c，d∈Z，且fm（a）=fm（b），fm（c）=fm（d），则fm（a+c）=fm（b+d）
④若a，b，c，d∈Z，且fm（a）=fm（b），fm（c）=fm（d），则fm（ac）=fm（bd）
若曲线f（x）=ax2-lnx存在垂直于y轴的切线，则实数a的取值范围是
 
．
已知集合M={1，2，3，…，100}，A是集合M的非空子集，把集合A中的各元素之和记作S（A）．
①满足S（A）=8的集合A的个数为
 
；
②S（A）的所有不同取值的个数为
 
．
已知f（x）是二次函数，关于x的方程mf2（x）+nf（x）+p=0（m，n，p都是实数）有四个不同的实数根，且它们从小到大的顺序为：x1＜x2＜x3＜x4，则x1-x2-x3+x4的值为
 
．
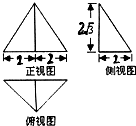一个几何体的三视图如图所示，其中正视图是正三角形，则该几何体的三个侧棱与地面所成的角的集合为
 
．
在平行四边形ABCD中，
AB
=
a
，
AD
=
b
，
AN
=3
NC
，M为BC的中点，则
MN
=（　　）
A、-
1
4
a
+
1
4
b
B、-
1
2
a
+
1
2
b
C、
a
+
1
2
b
D、-
3
4
a
+
3
4
b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网