题目内容
设函数f(x)=x|x|+bx+c,
①函数f(x)在R上有最小值;
②当b>0时,函数f(x)在R上是单调增函数;
③函数f(x)的图象关于点(0,c)对称;
④当b<0时,方程f(x)=0有三个不同实数根的充要条件是b2>4|c|.
则上述命题中所有正确命题的序号是 .
①函数f(x)在R上有最小值;
②当b>0时,函数f(x)在R上是单调增函数;
③函数f(x)的图象关于点(0,c)对称;
④当b<0时,方程f(x)=0有三个不同实数根的充要条件是b2>4|c|.
则上述命题中所有正确命题的序号是
考点:命题的真假判断与应用
专题:计算题,阅读型,分类讨论,函数的性质及应用
分析:①当b<0时,可以根据函数的值域加以判断函数f(x)在R上是否有最小值;
②当b>0时,把函数f(x)=|x|x+bx+c分x≥0和x<0两种情况讨论,转化为二次函数求单调性;
③函数f(x)的图象关于点(0,c)对称,可以根据函数图象的平移解决;
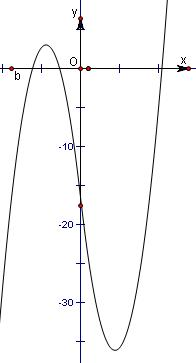
④当b<0时,方程f(x)=0有三个不同实数根,考虑函数f(x)与x轴有三个交点,如图,其充要条件是函数y=f(x)的极大值大于0且极小值小于0,即可得到结论.
②当b>0时,把函数f(x)=|x|x+bx+c分x≥0和x<0两种情况讨论,转化为二次函数求单调性;
③函数f(x)的图象关于点(0,c)对称,可以根据函数图象的平移解决;
④当b<0时,方程f(x)=0有三个不同实数根,考虑函数f(x)与x轴有三个交点,如图,其充要条件是函数y=f(x)的极大值大于0且极小值小于0,即可得到结论.
解答:
 解:对于①,当b<0时,f(x)=|x|x+bx+c
解:对于①,当b<0时,f(x)=|x|x+bx+c
=
,值域是R,
故函数f(x)在R上没有最小值,则①错;
对于②,当b>0时,f(x)=|x|x+bx+c=
,
知函数f(x)在R上是单调增函数,则②对;
对于③,若f(x)=|x|x+bx,
那么函数f(x)是奇函数(f(-x)=-f(x)),
也就是说函数f(x)的图象关于(0,0)对称.
而函数f(x)=|x|x+bx+c的图象是由函数f(x)=|x|x+bx的图象沿y轴移动,故图象一定是关于(0,c)对称的,则③对;
对于④,当b<0时,方程f(x)=0有三个不同实数根,
考虑函数f(x)与x轴有三个交点,如图,
其充要条件是函数y=f(x)的极大值大于0且极小值小于0,
即
<0,
>0,即有b2>4c且b2>-4c,即有b2>4|c|成立,
则④对.
故答案为:②③④
 解:对于①,当b<0时,f(x)=|x|x+bx+c
解:对于①,当b<0时,f(x)=|x|x+bx+c=
|
故函数f(x)在R上没有最小值,则①错;
对于②,当b>0时,f(x)=|x|x+bx+c=
|
知函数f(x)在R上是单调增函数,则②对;
对于③,若f(x)=|x|x+bx,
那么函数f(x)是奇函数(f(-x)=-f(x)),
也就是说函数f(x)的图象关于(0,0)对称.
而函数f(x)=|x|x+bx+c的图象是由函数f(x)=|x|x+bx的图象沿y轴移动,故图象一定是关于(0,c)对称的,则③对;
对于④,当b<0时,方程f(x)=0有三个不同实数根,
考虑函数f(x)与x轴有三个交点,如图,
其充要条件是函数y=f(x)的极大值大于0且极小值小于0,
即
| 4c-b2 |
| 4 |
| -4c-b2 |
| -4 |
则④对.
故答案为:②③④
点评:本题考查了分段函数的单调性、对称性和最值等问题,对于含有绝对值的一类问题,通常采取去绝对值的方法解决,体现了分类讨论的数学思想;函数的对称性问题一般转化为函数的奇偶性加以分析,再根据函数图象的平移解决,体现了转化、运动的数学思想;对于存在性的命题研究,一般通过特殊值法来解决.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知点P是抛物线y2=4x上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当|a|>4时,|PA|+|PM|的最小值是( )
A、
| ||
B、
| ||
| C、a+3 | ||
D、
|
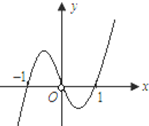 已知函数y=
已知函数y=| f′(x) |
| x |
| A、f′(1)=f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf′(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |
已知两异面直线a,b的夹角是15°,过空间一点P作直线l,使得l与a,b的夹角均为8°,那么这样的直线l有( )
| A、3条 | B、2条 | C、1条 | D、0条 |
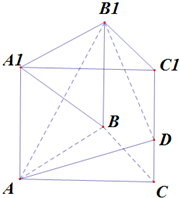
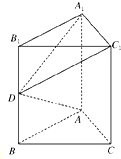 如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1.
如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1.