题目内容
已知点P是抛物线y2=4x上的动点，点P在y轴上的射影是M，点A 的坐标是（4，a），则当|a|＞4时，|PA|+|PM|的最小值是（ ）
A、
| ||
B、
| ||
| C、a+3 | ||
D、
|
考点：抛物线的简单性质
专题：圆锥曲线中的最值与范围问题
分析：先看当x=4时根据抛物线方程求得纵坐标的绝对值，而|a|＞4，明A（4，a）是在抛物线之外抛物线焦点和准线可求得，延长PM交L：x=-1于点N，必有：|PM|=|PN|-|MN|=|PN|-1根据抛物线的定义，可知：抛物线上的点P到准线x=-1的距离等于其到焦点F（1，0）的距离进而判断出|PA|+|PM|=|PF|+|PA|-1，只需求出|PF|+|PA|的最小值即可．由于A在抛物线之外，可由图象的几何位置判断出：AF必与抛物线交于一点，设此点为P'，看p和P'的重合与不重合两种情况分别求得最小值，最后综合可得答案．
解答：
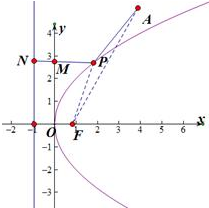
解：当x=4时，y2=4×4=16，所以y=±4，即|y|=4，因为|a|＞4，所以点A在抛物线的外侧，延长PM交直线x=-1，由抛物线的定义可知|PN|=|PM|+1=|PF|，当，三点A，P，F共线时，|PA|+|PF|最小，此时为|PA|+|PF|=|AF|，又焦点坐标为F（1，0），所以|AF|=
=
，即|PM|+1+|PA|的最小值为
，所以|PM|+|PA|的最小值为
-1，
故选：B．
解：当x=4时，y2=4×4=16，所以y=±4，即|y|=4，因为|a|＞4，所以点A在抛物线的外侧，延长PM交直线x=-1，由抛物线的定义可知|PN|=|PM|+1=|PF|，当，三点A，P，F共线时，|PA|+|PF|最小，此时为|PA|+|PF|=|AF|，又焦点坐标为F（1，0），所以|AF|=
| (4-1)2+a2 |
| 9+a2 |
| a2+9 |
| a2+9 |
故选：B．
点评：本题主要考查了抛物线的应用，以及抛物线定义的应用．考查了学生对抛物线定义的理解和应用．
练习册系列答案
名校课堂系列答案
相关题目
点A（1，2，3）关于xOy平面的对称点为A1，则A1坐标为（ ）
| A、（1，2，-3） |
| B、（-1，-2，-3） |
| C、（-1，-2，3） |
| D、（1，-2，3） |
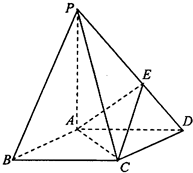如图，在底面为棱形的四棱锥P-ABCD在那个，∠ABC=60°，PA=AC=1，PB=PD=
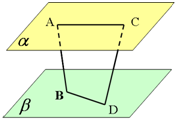已知AB、CD是夹在平行平面α、β间的异面线段，A，C∈α，B，D∈β，且AC=6，BD=8，AB=CD=10，AB和CD成60°角．求异面直线AC和BD所成的角．
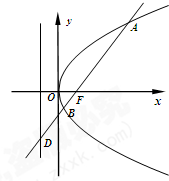如图，已知抛物线C：y2=4x，过焦点F斜率大于零的直线l交抛物线于A、B两点，且与其准线交于点D．