题目内容
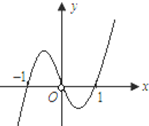 已知函数y=
已知函数y=| f′(x) |
| x |
| A、f′(1)=f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf′(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |
考点:利用导数研究函数的单调性,函数的图象,导数的运算
专题:导数的综合应用
分析:根据函数单调性和导数之间的关系,分别进行判断即可.
解答:
解:A.由图象可知x=1或-1时,f′(1)=f′(-1)=0成立.
B.当x<-1时,
<0,此时f′(x)>0,当-1<x<0时,
>0,此时f′(x)<0,故当x=-1时,函数f(x)取得极大值,成立.
C.方程xf′(x)=0等价为x2•
=0,故xf′(x)=0有两个,故C错误.
D.当0<x<1时,
<0,此时f′(x)<0,当x>1时,
>0,此时f′(x)>0,故当x=1时,函数f(x)取得极小值,成立.
故选:C
B.当x<-1时,
| f′(x) |
| x |
| f′(x) |
| x |
C.方程xf′(x)=0等价为x2•
| f′(x) |
| x |
D.当0<x<1时,
| f′(x) |
| x |
| f′(x) |
| x |
故选:C
点评:本题主要考查导数的应用,利用函数单调性和导数之间的关系是解决本题的关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、在统计里,从总体中抽取的一部分个体叫做总体的一个样本,样本中个体的数目叫做样本的容量 |
| B、一组数据的平均数一定大于这组数据中的每个数据 |
| C、平均数、众数与中位数从不同的角度描述了一组数据的集中趋势 |
| D、一组数据的方差越大,说明这组数据的波动性越大 |
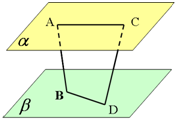 已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.
已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.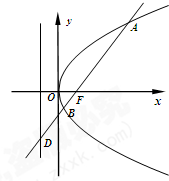 如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.
如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.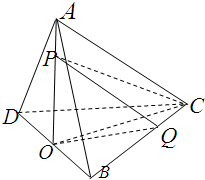 如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为
如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为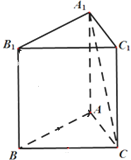 在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证:
在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证: