题目内容
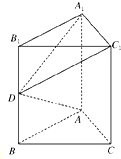 如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1.
如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1.考点:直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:根据直棱柱的几何特征,结合∠B1A1C1=90°,可证得A1C1⊥平面A1B1BA,进而AD⊥A1C1,由勾股定理可得A1D⊥AD,最后由线面垂直的判定定理得到AD⊥平面A1DC1.
解答:
证明:∵AA1⊥平面A1B1C1,
∴AA1⊥A1C1
又A1C1⊥A1B1,
∴A1C1⊥平面A1B1BA
∴AD⊥A1C1
∵AD=
,A1D=
,AA1=2,
由AD2+A1D2=AA12,
得A1D⊥AD
∵A1C1∩A1D=A1
∴AD⊥平面A1DC1
∴AA1⊥A1C1
又A1C1⊥A1B1,
∴A1C1⊥平面A1B1BA
∴AD⊥A1C1
∵AD=
| 2 |
| 2 |
由AD2+A1D2=AA12,
得A1D⊥AD
∵A1C1∩A1D=A1
∴AD⊥平面A1DC1
点评:本题考查直线与平面垂直的判定,考查空间想象能力,逻辑思维能力,计算能力,属于基本知识的考查,属于中档题.

练习册系列答案
相关题目
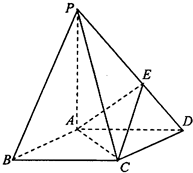 如图,在底面为棱形的四棱锥P-ABCD在那个,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面为棱形的四棱锥P-ABCD在那个,∠ABC=60°,PA=AC=1,PB=PD=| 2 |
(1)求证:PA⊥平面ABCD;
(2)求二面角E-AC-D的正弦值.
在空间中,a,b是不重合的直线,α,β是不重合的平面,则下列条件中可推出a∥b的是( )
| A、a?α,b?β,α∥β |
| B、a∥α,b?β |
| C、a⊥α,b⊥β |
| D、a⊥α,b?α |
已知函数f(x)=mx2-2(3-m)x+4,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是( )
| A、(0,3] |
| B、(0,9) |
| C、(1,9) |
| D、(-∞,9] |
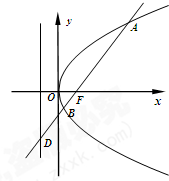 如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.
如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.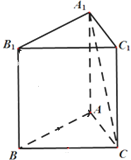 在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证:
在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证: