题目内容
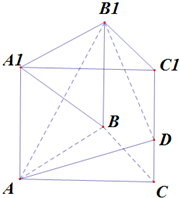
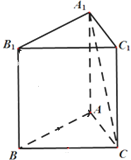
如图，正三棱柱中，所有的棱长都为2，D为CC1的中点，求证：A1B⊥平面AB1D．
考点：直线与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：取AC中点O，连结BO，由已知条件推导出BO⊥平面ACA1C1，连结A1O，则A1O⊥AD，BA1⊥AD，AB1⊥A1B，由此能证明AB1⊥平面A1BD．
解答：
解：取AC中点O，连接BO，
∵△ABC为正三角形，∴BO⊥AC．
∵正三棱柱ABC-A1B1C1中，平面ABC⊥平面ACA1C1，
∴BO⊥平面ACA1C1，BO⊥AD，
连接A1O，在正方形AA1C1C中，O、D分别为AC、CC1的中点，
∴A1O⊥AD，
∴AD⊥A1B．
在正方形ABB1A1中，AB1⊥A1B，
∴AB1⊥平面A1BD．
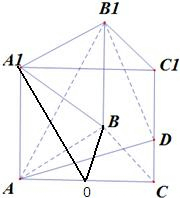
∵△ABC为正三角形，∴BO⊥AC．
∵正三棱柱ABC-A1B1C1中，平面ABC⊥平面ACA1C1，
∴BO⊥平面ACA1C1，BO⊥AD，
连接A1O，在正方形AA1C1C中，O、D分别为AC、CC1的中点，
∴A1O⊥AD，
∴AD⊥A1B．
在正方形ABB1A1中，AB1⊥A1B，
∴AB1⊥平面A1BD．
点评：本题考查直线与平面垂直的证明，解题时要认真审题，注意空间思维能力的培养，属于基本知识的考查，属于中档题．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
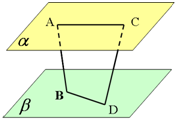已知AB、CD是夹在平行平面α、β间的异面线段，A，C∈α，B，D∈β，且AC=6，BD=8，AB=CD=10，AB和CD成60°角．求异面直线AC和BD所成的角．
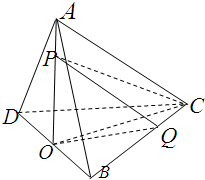如图，在三棱锥A-BCD中，BC=DC=AB=AD=2，BD=2，平面ABD⊥平面BCD，O为BD中点，点P，Q分别为线段AO，BC上的动点（不含端点），且AP=CQ，则三棱锥P-QCO体积的最大值为
在直三棱柱（侧棱与底面垂直的三棱柱）ABC-A1B1C1中，AB=8，AC=6，BC=10．求证：已知α，β是平面，a，b，c是直线，O是点．下列五个命题：
①若α∥β，a?α，b?β，则a∥b；
②若a∥b，a⊥c，则b⊥c；
③若a∥α，b?α，则a∥b；
④若a∥α，b∥α，则a∥b；
⑤若a∩b=O，a∥α，则b与α平行或相交．
其中正确的有（ ）
①若α∥β，a?α，b?β，则a∥b；
②若a∥b，a⊥c，则b⊥c；
③若a∥α，b?α，则a∥b；
④若a∥α，b∥α，则a∥b；
⑤若a∩b=O，a∥α，则b与α平行或相交．
其中正确的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
曲线
+
=1与曲线
+
=1（m＜3）的（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4-m |
| y2 |
| 3-m |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |