题目内容
5. 如图,已知圆心为C(4,3)的圆经过原点O.
如图,已知圆心为C(4,3)的圆经过原点O.(Ⅰ)求圆C的方程;
(Ⅱ)设直线3x-4y+m=0与圆C交于A,B两点.若|AB|=8,求m的值.
分析 (Ⅰ)由两点间距离公式求出圆C的半径,由此能求出圆C的方程.
(Ⅱ)作CD⊥AB于D,则CD平分线段AB,从在则 $|AD|\;=\frac{1}{2}|AB|\;=4$,由勾股定理求出CD,由点到直线的距离公式求出CD,由此能求出m.
解答  (本小题满分13分)
(本小题满分13分)
(Ⅰ)解:∵圆心为C(4,3)的圆经过原点O,
∴圆C的半径 $|OC|\;=\sqrt{{3^2}+{4^2}}=5$,(3分)
∴圆C的方程为(x-4)2+(y-3)2=25.(5分)
(Ⅱ)解:∵直线3x-4y+m=0与圆C交于A,B两点.若|AB|=8,
作CD⊥AB于D,则CD平分线段AB,
∴$|AD|\;=\frac{1}{2}|AB|\;=4$.(7分)
在直角三角形ADC中,$|CD|\;=\sqrt{|AC{|^2}-|AD{|^2}}=3$.(9分)
由点到直线的距离公式,得$|CD|\;=\frac{|3×4-4×3+m|}{{\sqrt{{3^2}+{4^2}}}}=\frac{|m|}{5}$,(11分)
∴$\frac{|m|}{5}=3$,(12分)
解得m=±15.(13分)
点评 本题考查圆的方程的求法,考查实数值的求法,是中档题,解题时要认真审题,注意圆的性质、点到直线的距离公式的合理运用.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
10.设命题p:“若$sinα=\frac{1}{2}$,则$α=\frac{π}{6}$”,命题q:“若a>b,则$\frac{1}{a}<\frac{1}{b}$”,则( )
| A. | “p∧q”为真命题 | B. | “p∨q”为假命题 | C. | “¬q”为假命题 | D. | 以上都不对 |
14.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为45°,且|$\overrightarrow{a}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2.则|$\overrightarrow{b}$|等于( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
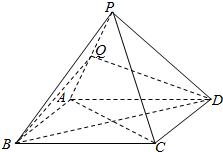 如图,四棱锥P-ABCD的底面ABCD为菱形,Q是棱PA的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,Q是棱PA的中点. 已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\sqrt{2}$,一条准线方程为x=$\frac{\sqrt{2}}{2}$,直线l与双曲线右支及双曲线的渐近线交于A、B、C、D四点,四个点的顺序如图所示.
已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\sqrt{2}$,一条准线方程为x=$\frac{\sqrt{2}}{2}$,直线l与双曲线右支及双曲线的渐近线交于A、B、C、D四点,四个点的顺序如图所示.