题目内容
10.设命题p:“若$sinα=\frac{1}{2}$,则$α=\frac{π}{6}$”,命题q:“若a>b,则$\frac{1}{a}<\frac{1}{b}$”,则( )| A. | “p∧q”为真命题 | B. | “p∨q”为假命题 | C. | “¬q”为假命题 | D. | 以上都不对 |
分析 分别判断出p,q的真假,从而判断出复合命题的真假即可.
解答 解:命题p:“若$sinα=\frac{1}{2}$,则$α=\frac{π}{6}$”是假命题,
命题q:“若a>b,则$\frac{1}{a}<\frac{1}{b}$”如:a=1,b=-1,
故命题q是假命题,
故p∨q是假命题,
故选:B.
点评 本题考察了复合命题的判断,是一道基础题.

练习册系列答案
相关题目
18.如图,在长方体ABCD-A1B1C1D1中,AA1=2AB,AB=BC,则下列结论中正确的是( )
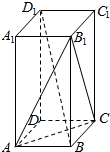

| A. | BD1∥B1C | B. | A1D1∥平面AB1C | C. | BD1⊥AC | D. | BD1⊥平面AB1C |
20.已知函数f(x)=$\left\{\begin{array}{l}{kx+2,x≥0}\\{(\frac{1}{2})^{x},x<0}\end{array}\right.$,则下列关于函数y=f[f(x)]-$\frac{3}{2}$的零点个数的判断正确的是( )
| A. | 当k≥0时,有1个零点;当k<0时,有2个零点 | |
| B. | 当k≥0时,没有零点;当-$\frac{1}{2}$<k≤-$\frac{1}{4}$时,有3个零点,当k≤-$\frac{1}{2}$或-$\frac{1}{4}$<k<0有2个零点 | |
| C. | 当k≥0时,没有零点;当-$\frac{1}{2}$<k<0时,有3个零点,当k≤-$\frac{1}{2}$有2个零点 | |
| D. | 当k≥0时,没有零点;当-$\frac{1}{2}$≤k<-$\frac{1}{4}$时,有3个零点,当k<-$\frac{1}{2}$或-$\frac{1}{4}$≤k<0有2个零点 |
 如图,在直三棱柱ABC-A1B1C1中,已知A1C1⊥B1C1,CC1=2BC=2.
如图,在直三棱柱ABC-A1B1C1中,已知A1C1⊥B1C1,CC1=2BC=2. 如图,已知圆心为C(4,3)的圆经过原点O.
如图,已知圆心为C(4,3)的圆经过原点O.