题目内容
13.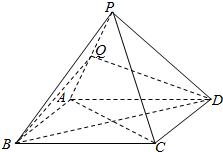 如图,四棱锥P-ABCD的底面ABCD为菱形,Q是棱PA的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,Q是棱PA的中点.(Ⅰ)求证:PC∥平面BDQ;
(Ⅱ)若PB=PD,求证:平面PAC⊥平面BDQ.
分析 (Ⅰ)设AC交BD于点O,连结OQ,证明OQ∥PC.即可利用直线与平面平行的判定定理证明PC∥平面BDQ.
(Ⅱ)连结OP.说明BD⊥AC,BD⊥PO,然后证明BD⊥平面PAC,利用平面与平面垂直的判定定理证明平面PAC⊥平面BDQ.
解答 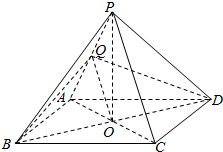 (本小题满分13分)
(本小题满分13分)
(Ⅰ)证明:设AC交BD于点O,连结OQ.(1分)
因为 底面ABCD为菱形,
所以 O为AC中点.
因为 Q是PA的中点,
所以 OQ∥PC.(4分)
因为 OQ?平面BDQ,PC?平面BDQ,
所以PC∥平面BDQ.(5分)
(Ⅱ)证明:连结OP.(6分)
因为 底面ABCD为菱形,
所以 BD⊥AC,O为BD中点.(8分)
因为 PB=PD,
所以 BD⊥PO.(10分)
又因为:AO∩AC=0,
所以 BD⊥平面PAC.(11分)
因为 BD?平面BDQ,
所以 平面PAC⊥平面BDQ.(13分).
点评 本题考查平面与平面垂直的判定定理的应用,直线与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
8.在空间中,给出下列四个命题:
①平行于同一个平面的两条直线互相平行;
②垂直于同一个平面的两个平面互相平行;
③平行于同一条直线的两条直线互相平行;
④垂直于同一条直线的两条直线互相平行.
其中真命题的序号是( )
①平行于同一个平面的两条直线互相平行;
②垂直于同一个平面的两个平面互相平行;
③平行于同一条直线的两条直线互相平行;
④垂直于同一条直线的两条直线互相平行.
其中真命题的序号是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
18.如图,在长方体ABCD-A1B1C1D1中,AA1=2AB,AB=BC,则下列结论中正确的是( )
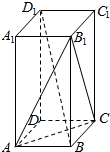

| A. | BD1∥B1C | B. | A1D1∥平面AB1C | C. | BD1⊥AC | D. | BD1⊥平面AB1C |
 如图,在直三棱柱ABC-A1B1C1中,已知A1C1⊥B1C1,CC1=2BC=2.
如图,在直三棱柱ABC-A1B1C1中,已知A1C1⊥B1C1,CC1=2BC=2. 如图,已知圆心为C(4,3)的圆经过原点O.
如图,已知圆心为C(4,3)的圆经过原点O.