题目内容
6.命题p:直线y=kx+3与圆x2+y2=1相交于A,B两点;命题q:曲线$\frac{{x}^{2}}{k-6}$-$\frac{{y}^{2}}{k}$=1表示焦点在y轴上的双曲线,若p∧q为真命题,求实数k的取值范围.分析 命题p:直线y=kx+3与圆x2+y2=1相交于A,B两点,可得圆心到直线的距离$d=\frac{{|{k•0-0+3}|}}{{\sqrt{{k^2}+1}}}<1$,解得k范围.命题q:曲线$\frac{{x}^{2}}{k-6}$-$\frac{{y}^{2}}{k}$=1表示焦在y轴上的双曲线,可得$\left\{\begin{array}{l}{k-6<0}\\{k<0}\end{array}\right.$,解得k范围.由于p∧q为真命题,可得p,q均为真命题,即可得出.
解答 解:∵命题p:直线y=kx+3与圆x2+y2=1相交于A,B两点,
∴圆心到直线的距离$d=\frac{{|{k•0-0+3}|}}{{\sqrt{{k^2}+1}}}<1$,∴$k>2\sqrt{2}或k<-2\sqrt{2}$,(5分)
∵命题q:曲线$\frac{{x}^{2}}{k-6}$-$\frac{{y}^{2}}{k}$=1表示焦在y轴上的双曲线,
∴$\left\{\begin{array}{l}{k-6<0}\\{k<0}\end{array}\right.$,解得k<0,(10分)
∵p∧q为真命题,∴p,q均为真命题,
∴$\left\{\begin{array}{l}{k>2\sqrt{2}或k<-2\sqrt{2}}\\{k<0}\end{array}\right.$,
解得k<-2$\sqrt{2}$.(13分)
点评 本题考查了直线与圆的位置关系、双曲线的标准方程及其性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
17.已知等比数列{an}中,a1+a3=10,a4+a6=$\frac{5}{4}$,则该数列的公比q为( )
| A. | 2 | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
14.设m、n是两条不同的直线,α、β是两个不同的平面,则( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥α,m∥β,则α∥β | C. | 若m∥n,n⊥α,则m⊥α | D. | 若m∥α,α⊥β,则m⊥β |
11.在△ABC中,a、b、c分别为角A、B、C所对的边,cosA=$\frac{4}{5}$,b=2,面积S=3,则a为( )
| A. | $3\sqrt{5}$ | B. | $\sqrt{17}$ | C. | $\sqrt{21}$ | D. | $\sqrt{13}$ |
15.设集合P={x|x>1},Q={x|x>0},则下列结论正确的是( )
| A. | P?Q | B. | Q?P | C. | P=Q | D. | P∪Q=R |
16.阅读如图的程序框图,运行相应的程序,若$f(x)=cos\frac{π}{3}x$,则输出的S的值为( )
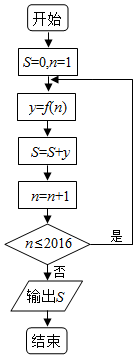

| A. | 0 | B. | 671.5 | C. | 671 | D. | 672 |