题目内容
16.若函数f(x)=$\frac{lg(\sqrt{a+9{x}^{2}}-3x)}{x}$的图象关于y轴对称,则a的值为1.分析 利用函数图象的对称性得出f(-x)=f(x),利用特殊值f(-1)=f(1)代入求解即可.
解答 解:∵函数f(x)=$\frac{lg(\sqrt{a+9{x}^{2}}-3x)}{x}$的图象关于y轴对称
∴f(-x)=f(x)
即x=1时f(-1)=f(1)
-lg($\sqrt{a+9}$+3)=lg($\sqrt{a+9}$-3)
$\frac{1}{\sqrt{a+9}+3}$=$\sqrt{a+9}$-3,
(a+9)=10
a=1
故答案为:1
点评 本题简单的考查了函数的性质,与函数图象,关键是判断出是偶函数即可.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
7.若方程${x^2}+\frac{y^2}{m}=4$表示焦点在x轴上的椭圆,则实数m的取值范围是( )
| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (1,+∞) |
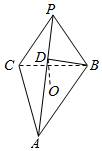 三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心.
三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心. 如图,AB是⊙O的直径,点P是⊙O圆周上异于A,B的一点,AD⊥⊙O所在的平面PAB,四边形ABCD是边长为2的正方形,连结PA,PB,PC,PD.
如图,AB是⊙O的直径,点P是⊙O圆周上异于A,B的一点,AD⊥⊙O所在的平面PAB,四边形ABCD是边长为2的正方形,连结PA,PB,PC,PD.