题目内容
11.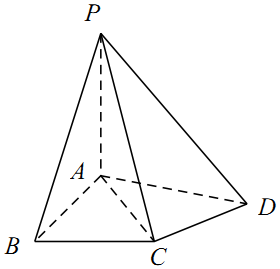 如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.(Ⅰ)点E在棱PC上,试确定点E的位置,使得PD⊥平面ABE;
(Ⅱ)求二面角A-PD-C的余弦值.
分析 (Ⅰ)以A为坐标原点,射线AB,AD,AP分别为x,y,z轴的正方向,建立空间直角坐标系,利用向地能求出当E为PC中点时,PD⊥平面ABE.
(Ⅱ)求出平面PCD的一个法向量和平面PAD的一个法向量,利用向量法能求出二面角A-PD-C的余弦值.
解答 解:(Ⅰ)∵PC=$\sqrt{2}$PA=$\sqrt{2}AC$,∴PA⊥AC,
又∵平面PAC⊥平面ABCD,平面PAC∩平面ABCD=AC,
∴PA⊥平面ABCD,∴PA⊥AB,PA⊥AD,
以A为坐标原点,射线AB,AD,AP分别为x,y,z轴的正方向,
建立空间直角坐标系,设PA=2,
则B(2,0,0),C(1,$\sqrt{3}$,0),D(0,$\frac{4\sqrt{3}}{3}$,0),P(0,0,2).(2分)
$\overrightarrow{AB}•\overrightarrow{AD}=0$,故PD⊥AB,
设$\overrightarrow{AE}$=$\overrightarrow{AP}+λ\overrightarrow{PC}$,
∵AE⊥PD,∴$\overrightarrow{AE}•\overrightarrow{PD}=0$,即$\overrightarrow{AP}•\overrightarrow{PD}+λ\overrightarrow{PC}•\overrightarrow{PD}$=0,
即-4+λ•8=0,即$λ=\frac{1}{2}$,即当E为PC中点时,AE⊥PD,
则PD⊥平面ABE.所以当E为PC中点时,PD⊥平面ABE.…(6分)
(Ⅱ)设平面PCD的一个法向量$\overrightarrow{n}$=(x,y,z),
$\overrightarrow{PC}=(1,\sqrt{3},-2)$,$\overrightarrow{PD}=(0,\frac{4\sqrt{3}}{3},-2)$,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PC}=x+\sqrt{3}y-2z=0}\\{\overrightarrow{n}•\overrightarrow{PD}=\frac{4\sqrt{3}}{3}y-2z=0}\end{array}\right.$,
令x=1,则$\overrightarrow{n}$=(1,$\sqrt{3},2$),
再取平面PAD的一个法向量$\overrightarrow{m}$=(1,0,0).…(9分)
则cos<$\overrightarrow{n},\overrightarrow{m}$>=$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=$\frac{\sqrt{2}}{4}$,
故二面角A-PD-C的余弦值为$\frac{\sqrt{2}}{4}$.…(12分)
点评 本题考查满足条件的点的位置的确定与求法,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | [$\frac{3}{8}$,$\frac{11}{12}$]∪[$\frac{11}{8}$,$\frac{19}{12}$] | B. | ($\frac{1}{4}$,$\frac{5}{12}$]∪[$\frac{5}{8}$,$\frac{3}{4}$] | ||
| C. | [$\frac{3}{8}$,$\frac{7}{12}$]∪[$\frac{7}{8}$,$\frac{11}{12}$] | D. | ($\frac{1}{4}$,$\frac{3}{4}$]∪[$\frac{9}{8}$,$\frac{17}{12}$] |
| A. | (0,+∞) | B. | (1,+∞) | C. | (2,+∞) | D. | (-∞,2) |
| A. | -$\frac{33}{15}$ | B. | $\frac{33}{15}$ | C. | -$\frac{33}{17}$ | D. | $\frac{33}{17}$ |
| A. | {3,5} | B. | {1,3,4,5,6,7,8} | C. | {2,8} | D. | {1,7} |
| A. | $\frac{3}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{2}}{4}$ |
| A. | 若a>b,c>d,则ac>bd | B. | 若ab≥0,则|a+b|=|a|+|b| | ||
| C. | 若x>2,则函数y=x+$\frac{1}{x}$有最小值2 | D. | 若a<b<0,则a2<ab<b2 |
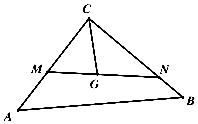 如图,等腰直角三角形ABC,点G是△ABC的重心,过点G作直线与CA,CB两边分别交于M,N两点,且$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,则λ+4μ的最小值为3.
如图,等腰直角三角形ABC,点G是△ABC的重心,过点G作直线与CA,CB两边分别交于M,N两点,且$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,则λ+4μ的最小值为3.