题目内容
3.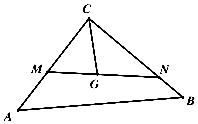 如图,等腰直角三角形ABC,点G是△ABC的重心,过点G作直线与CA,CB两边分别交于M,N两点,且$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,则λ+4μ的最小值为3.
如图,等腰直角三角形ABC,点G是△ABC的重心,过点G作直线与CA,CB两边分别交于M,N两点,且$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,则λ+4μ的最小值为3.
分析 由题意$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,从而化简可得$\frac{1}{3}$($\overrightarrow{CA}$+$\overrightarrow{CB}$)-λ$\overrightarrow{CA}$=x(μ$\overrightarrow{CB}$-$\frac{1}{3}$($\overrightarrow{CA}$+$\overrightarrow{CB}$)),从而可得$\frac{1}{λ}+\frac{1}{μ}$=3,然后利用基本不等式求最值.
解答 解:$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,
∵M,N,G三点共线,
∴$\overrightarrow{MG}$=x$\overrightarrow{GN}$,
∴$\overrightarrow{CG}$-$\overrightarrow{CM}$=x($\overrightarrow{CN}$-$\overrightarrow{CG}$),
∵点G是△ABC的重心,
∴$\overrightarrow{CG}$=$\frac{1}{3}$($\overrightarrow{CA}$+$\overrightarrow{CB}$),
∴$\frac{1}{3}$($\overrightarrow{CA}$+$\overrightarrow{CB}$)-λ$\overrightarrow{CA}$=x(μ$\overrightarrow{CB}$-$\frac{1}{3}$($\overrightarrow{CA}$+$\overrightarrow{CB}$)),
∴$\left\{\begin{array}{l}{\frac{1}{3}-λ=-\frac{1}{3}x}\\{\frac{1}{3}=xμ-\frac{1}{3}x}\end{array}\right.$,
解得,(1-3λ)(1-3μ)=1,可得$\frac{1}{λ}+\frac{1}{μ}$=3.
λ+4μ=$\frac{1}{3}$(λ+4μ)($\frac{1}{λ}+\frac{1}{μ}$)=$\frac{5}{3}+\frac{1}{3}•(\frac{λ}{μ}+\frac{4μ}{λ})$≥$\frac{5}{3}+\frac{1}{3}×2×\sqrt{\frac{γ}{μ}•\frac{4μ}{λ}}$=$\frac{5}{3}+\frac{4}{3}$=3.
(当且仅当$\frac{λ}{μ}=\frac{4μ}{λ}$,即λ=1,μ=$\frac{1}{2}$时,等号成立),
故λ+4μ的最小值为:3.
故答案为:3.
点评 本题考查了平面向量的线性运算的应用及共线定理的应用,同时考查了基本不等式在求最值中的应用.

| A. | 224 | B. | 218 | C. | 228 | D. | 258 |
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{3}}{10}$ |
| A. | 22014 | B. | 22015 | C. | 22016 | D. | 22017 |
| A. | ω≥1 | B. | ω≤-1 | C. | -1≤ω<0 | D. | 0<ω≤1 |
| A. | {1} | B. | {1,3} | C. | {3} | D. | {1,2,3} |
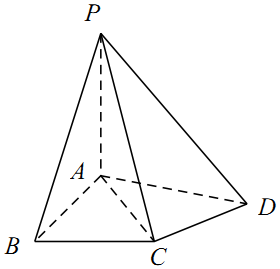 如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.