题目内容
6.已知Sn为等差数列{an}的前n项和,a5=2,an-1+an+1=a5an(n≥2)且a3是a1与-$\frac{8}{5}$的等比数列.(1)求数列{an}的通项公式;
(2)若a1为整数,bn=$\frac{n}{(2{S}_{n}+23n)(n+1)}$,求数列{bn}前n项和Tn.
分析 (1)根据a5=2,an-1+an+1=a5an(n≥2)且a3是a1与-$\frac{8}{5}$的等比中项得到首项和公差,得到通项公式.
(2)由(1)得到Sn,整理数列{bn},利用通项公式特点,利用裂项求和即可.
解答 解:(1)∵a5=2,an-1+an+1=a5an(n≥2),
∴an-1+an+1=2an(n≥2)∴数列{an}为等差数列.
设数列{an}的公差为d.∵a3是a1与-$\frac{8}{5}$的等比中项,∴a32=a1•-$\frac{8}{5}$.
∴(2-2d)2=-$\frac{8}{5}$(2-4d)
∴(5d-3)(d-3)=0
∴d=$\frac{3}{5}$或d=3.
当d=$\frac{3}{5}$时,an=$\frac{3}{5}n$-1.
当d=3时,an=3n-13.
(2)若a1为整数,则an=3n-13,
∴${S}_{n}=\frac{n(3n-23)}{2}$,
∴2Sn+23n=3n2,
bn=$\frac{n}{(2{S}_{n}+23n)(n+1)}$=$\frac{1}{3n(n+1)}=\frac{1}{3}(\frac{1}{n}-\frac{1}{n+1})$,
数列{bn}前n项和Tn=$\frac{1}{3}$(1-$\frac{1}{2}$$+\frac{1}{2}-\frac{1}{3}$$+\frac{1}{3}-$…$+\frac{1}{n}-\frac{1}{n+1}$)
=$\frac{1}{3}×$(1-$\frac{1}{n+1}$)=$\frac{n}{3n+3}$.
点评 本题考查了数列的递推关系式以及利用公式法和裂项对数列求和;关键是正确利用等差中项和等比中项求出数列的通项公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若不等式|x-2|+|x+3|>a恒成立,则a的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,5) | D. | (5,+∞) |
17.已知集合M={x|x2-2x<0},N={x|x-1>0},则M∩N=( )
| A. | {x|1<x<2} | B. | {x|0<x<1} | C. | {x|x>2} | D. | {x|x<0} |
14.已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若${S}_{△ABC}=3{S}_{△BC{F}_{2}}$,则椭圆的离心率为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{3}}{10}$ |
1.某几何体的三视图如图所示,该几何体的体积为( )


| A. | 24 | B. | $\frac{70}{3}$ | C. | 20 | D. | $\frac{68}{3}$ |
18.若数列{an}满足an+2=2•$\frac{{{a_{n+1}}}}{a_n}$(n∈N*),且a1=1,a2=2,则数列{an}的前2016项之积为( )
| A. | 22014 | B. | 22015 | C. | 22016 | D. | 22017 |
15.若y=tanωx在$(-\frac{π}{2},\frac{π}{2})$内为减函数,则( )
| A. | ω≥1 | B. | ω≤-1 | C. | -1≤ω<0 | D. | 0<ω≤1 |
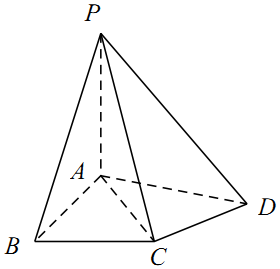 如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.