题目内容
20.设正数x,y满足x2+$\frac{{y}^{2}}{2}$=1,则x•$\sqrt{1+{y}^{2}}$的最大值为( )| A. | $\frac{3}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{2}}{4}$ |
分析 构造思想,再利用基本不等式的性质即可得出.
解答 解:由题意x>0,y>0,
x•$\sqrt{1+{y}^{2}}$=$\sqrt{{x}^{2}(1+{y}^{2})}=\sqrt{{x}^{2}•2(\frac{1}{2}+\frac{{y}^{2}}{2})}$=$\sqrt{2}•\sqrt{{x}^{2}(\frac{1}{2}+\frac{{y}^{2}}{2})}$$≤\sqrt{2}×\frac{{x}^{2}+\frac{1}{2}+\frac{{y}^{2}}{2}}{2}$,
∵x2+$\frac{{y}^{2}}{2}$=1,
∴x•$\sqrt{1+{y}^{2}}$$≤\sqrt{2}×\frac{{x}^{2}+\frac{1}{2}+\frac{{y}^{2}}{2}}{2}$=$\sqrt{2}×\frac{3}{4}=\frac{3\sqrt{2}}{4}$
故x•$\sqrt{1+{y}^{2}}$的最大值为$\frac{3\sqrt{2}}{4}$.
故选D.
点评 本题考查了构造思想,凑出已知条件以及基本不等式的性质.属于中档题.

练习册系列答案
相关题目
10.函数$f(x)={2}^{x}+\frac{1}{4•{2}^{x}}$的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
15.若y=tanωx在$(-\frac{π}{2},\frac{π}{2})$内为减函数,则( )
| A. | ω≥1 | B. | ω≤-1 | C. | -1≤ω<0 | D. | 0<ω≤1 |
12.已知集合I={1,2,3,4},B={2,4},A={1},则A∪(∁IB)=( )
| A. | {1} | B. | {1,3} | C. | {3} | D. | {1,2,3} |
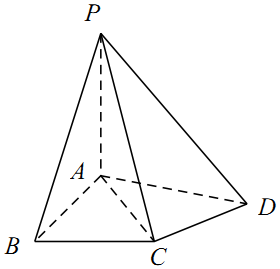 如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.