题目内容
在△ABC中，角A、B、C的对边分别为a、b、c，且满足（a+b）（sinA-sinB）-（a-c）sinC=0．
（1）求角B的大小；
（2）若cos2
=
+
，求tanC的值．
（1）求角B的大小；
（2）若cos2
| A |
| 2 |
| 1 |
| 2 |
| ||
| 10 |
考点：余弦定理,两角和与差的正切函数,正弦定理
专题：解三角形
分析：（1）△ABC中，由条件利用正弦定理可得 a2+c2-b2=a，求得cosB=
的值，即可求得B的值．
（2）由条件利用二倍角公式求得cosA=2cos2A-1的值，可得 sinA和tanA的值，再根据tanC=-tan（A+B），利用两角和的正切公式计算求得结果．
| a2+c2-b2 |
| 2ac |
（2）由条件利用二倍角公式求得cosA=2cos2A-1的值，可得 sinA和tanA的值，再根据tanC=-tan（A+B），利用两角和的正切公式计算求得结果．
解答：
解：（1）△ABC中，由（a+b）（sinA-sinB）-（a-c）sinC=0，利用正弦定理可得
（a+b）（a-b）-（a-c）c=0，即 a2+c2-b2=a，
∴cosB=
=
，∴B=
．
（2）∵cos2
=
+
，∴cosA=2cos2A-1=
，∴sinA=
，
∴tanA=
=2．
∴tanC=-tan（A+B）=-tan（
+A）=-
=
=
．
（a+b）（a-b）-（a-c）c=0，即 a2+c2-b2=a，
∴cosB=
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
| π |
| 3 |
（2）∵cos2
| A |
| 2 |
| 1 |
| 2 |
| ||
| 10 |
| ||
| 5 |
2
| ||
| 5 |
∴tanA=
| sinA |
| cosA |
∴tanC=-tan（A+B）=-tan（
| π |
| 3 |
tan
| ||
1-tan
|
| ||
1-2
|
8+5
| ||
| 11 |
点评：本题主要考查正弦定理、余弦定理、二倍角公式、两角和的正切公式、诱导公式的应用，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
集合A={x|x2＞1}，B={x|x+a≥0}，若∁UA⊆B，则实数a的取值范围是（ ）
| A、[-1，+∞） |
| B、[1，+∞） |
| C、（-∞，1] |
| D、（-∞，-1] |
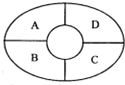如图某综艺节目现场设有A、B、C、D四个观众席，现有由3中不同颜色与2种不同款式组成的6中马甲安排给现场观众，要求每个观众席上的马甲相同，相邻观众席上的马甲的颜色与款式都不相同，则不同的安排方法种数为（ ）
函数y=Asin（ωx+φ），（A，ω，φ为常数，A＞0，ω＞0）在闭区间[0，