题目内容
已知f(x)=ax-lnx,x∈(0,e],g(x)=
+1其中e是自然常数,a∈R.
(1)讨论a=1时f(x)的单调性,极值;
(2)求证:在(1)的条件下,f(x+1)<g(x);
(3)是否存在实数a,使得f(x)的最小值是3,若存在,求出a的值,若不存在说明理由.
| x2 |
| 2 |
(1)讨论a=1时f(x)的单调性,极值;
(2)求证:在(1)的条件下,f(x+1)<g(x);
(3)是否存在实数a,使得f(x)的最小值是3,若存在,求出a的值,若不存在说明理由.
考点:导数在最大值、最小值问题中的应用,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(1)在定义域内解不等式f′(x)>0,f′(x)<0可得单调性,由极值定义可求得极值;
(2)f(x+1)<g(x),化为
-x+ln(x+1)>0,令h(x)=
-x+ln(x+1),利用导数可判断h(x)的单调性,由单调性可得结论;
(3)f′(x)=a-
=
,由此进行分类讨论能推导出存在a=e2.
(2)f(x+1)<g(x),化为
| x2 |
| 2 |
| x2 |
| 2 |
(3)f′(x)=a-
| 1 |
| x |
| ax-1 |
| x |
解答:
解:(1)a=1时,f′(x)=1-
,
∵x∈(0,e],
由f′(x)=1-
>0,得1<x≤e,
∴f(x)在(1,e]是单调递增.
由f′(x)=1-
<0,得0<x<1.
∴f(x)在(0,1)上单调递减.
∴f(x)有极小值f(1)=1,无极大值.
证明:(2)在(1)的条件下,f(x+1)<g(x),即为x+1-ln(x+1)<
+1,亦即
-x+ln(x+1)>0,
令h(x)=
-x+ln(x+1),h′(x)=x-1+
=
>0,
∴h(x)递增,h(x)>h(0)=0,即
-x+ln(x+1)>0;
(3)f′(x)=a-
=
,
①当a≤0时,f(x)在(0,e)上是减函数,
∴ae-1=3,a=
>0.
②当0<a<
时,f(x)在(0,e]上是减函数,
∴ae-1=3,a=
>
.
③当a≥
时,f(x)在(0,
]上是减函数,(
,e]上是增函数,
∴a×
-ln
=3,解得a=e2,
∴存在a=e2.
| 1 |
| x |
∵x∈(0,e],
由f′(x)=1-
| 1 |
| x |
∴f(x)在(1,e]是单调递增.
由f′(x)=1-
| 1 |
| x |
∴f(x)在(0,1)上单调递减.
∴f(x)有极小值f(1)=1,无极大值.
证明:(2)在(1)的条件下,f(x+1)<g(x),即为x+1-ln(x+1)<
| x2 |
| 2 |
| x2 |
| 2 |
令h(x)=
| x2 |
| 2 |
| 1 |
| x+1 |
| x2 |
| x+1 |
∴h(x)递增,h(x)>h(0)=0,即
| x2 |
| 2 |
(3)f′(x)=a-
| 1 |
| x |
| ax-1 |
| x |
①当a≤0时,f(x)在(0,e)上是减函数,
∴ae-1=3,a=
| 4 |
| e |
②当0<a<
| 1 |
| e |
∴ae-1=3,a=
| 4 |
| e |
| 1 |
| e |
③当a≥
| 1 |
| e |
| 1 |
| a |
| 1 |
| a |
∴a×
| 1 |
| a |
| 1 |
| a |
∴存在a=e2.
点评:本题考查利用导数研究函数的单调性,求闭区间上函数的最值,是中档题.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x-
,则( )
| 1 |
| x |
| A、函数f(x)的定义域是R |
| B、函数f(x)的值域是(-∞,0)∪(0,+∞) |
| C、函数f(x)在其定义域内是奇函数 |
| D、函数f(x)在其定义域内是增函数 |
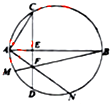 如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.
如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.