题目内容
已知函数f(x)=lnx-ax2-
(a∈R).
(Ⅰ)a=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若对定义域内的任意实数x1,x2(x1≠x2),都有
>5,求实数a的取值范围.
| 1 |
| x |
(Ⅰ)a=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若对定义域内的任意实数x1,x2(x1≠x2),都有
| f(x2)-f(x1) |
| x2-x1 |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)把a=0代入函数解析式,求出函数的导函数,进一步求得f(1)及f′(1)的值,由直线方程的点斜式得y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)由
>5,得到
>0,可得函数g(x)=f(x)-5x在(0,+∞)上是增函数,则其导函数大于等于0恒成立,分离参数a后得到2a≤
+
-
.令
=t换元后构造函数h(t)=t3+t2-5t,利用导数求其最小值,则实数a的取值范围可求.
(Ⅱ)由
| f(x2)-f(x1) |
| x2-x1 |
| f(x2)-5x2-[f(x1)-5x1] |
| x2-x1 |
| 1 |
| x3 |
| 1 |
| x2 |
| 5 |
| x |
| 1 |
| x |
解答:
解:(Ⅰ)a=0时,f(x)=lnx-
,则f′(x)=
+
,
f′(1)=2,
又f(1)=-1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为:
y-(-1)=2(x-1),
即2x-y-3=0;
(Ⅱ)∵
>5,
∴
-5>0,
∴
>0,
设g(x)=f(x)-5x,则g(x)在(0,+∞)上是增函数,
g(x)=lnx-ax2-
-5x,
g′(x)=
-2ax+
-5.
由g′(x)≥0,得2a≤
+
-
.
令
=t,
则h(t)=t3+t2-5t,
h′(t)=3t2+2t-5=(3t+5)(t-1),
∵t∈(0,1)时,h′(t)<0,
t∈(1,+∞)时,h′(t)>0,
∴h(t)min=h(1)=-3.
∴2a≤-3,
则a≤-
.
∴实数a的取值范围是(-∞,-
].
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
f′(1)=2,
又f(1)=-1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为:
y-(-1)=2(x-1),
即2x-y-3=0;
(Ⅱ)∵
| f(x2)-f(x1) |
| x2-x1 |
∴
| f(x2)-f(x1) |
| x2-x1 |
∴
| f(x2)-5x2-[f(x1)-5x1] |
| x2-x1 |
设g(x)=f(x)-5x,则g(x)在(0,+∞)上是增函数,
g(x)=lnx-ax2-
| 1 |
| x |
g′(x)=
| 1 |
| x |
| 1 |
| x2 |
由g′(x)≥0,得2a≤
| 1 |
| x3 |
| 1 |
| x2 |
| 5 |
| x |
令
| 1 |
| x |
则h(t)=t3+t2-5t,
h′(t)=3t2+2t-5=(3t+5)(t-1),
∵t∈(0,1)时,h′(t)<0,
t∈(1,+∞)时,h′(t)>0,
∴h(t)min=h(1)=-3.
∴2a≤-3,
则a≤-
| 3 |
| 2 |
∴实数a的取值范围是(-∞,-
| 3 |
| 2 |
点评:本题考查了利用导数研究曲线上某点处的切线方程,考查了利用导数求函数的最值,训练了分离变量法和构造函数法,是高考试卷中的压轴题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
设角α的终边过点P(-4,3),则2sinα+cosα的值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
| D、以上都不正确 |
设复数z=
,则
=( )
| 2i |
| 1-i |
. |
| z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
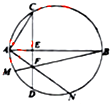 如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.
如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.