题目内容
集合A={x|x2＞1}，B={x|x+a≥0}，若∁UA⊆B，则实数a的取值范围是（ ）
| A、[-1，+∞） |
| B、[1，+∞） |
| C、（-∞，1] |
| D、（-∞，-1] |
考点：交、并、补集的混合运算
专题：集合
分析：求出集合A，利用集合的关系即可得到结论．
解答：
解：∵A={x|x2＞1}，
∴∁UA={x|x2≤1}={x|-1≤x≤1}，
∵B={x|x+a≥0}=B={x|x≥-a}，
若∁UA⊆B，
则-a≤-1，即a≥1，
故选：B
∴∁UA={x|x2≤1}={x|-1≤x≤1}，
∵B={x|x+a≥0}=B={x|x≥-a}，
若∁UA⊆B，
则-a≤-1，即a≥1，
故选：B
点评：本题主要考查集合的基本运算，比较基础．
练习册系列答案
相关题目
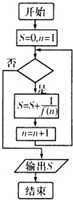
已知函数 f（x）=x2+x，执行如图所示的程序框图，若输出的结果是
，则判断框中的条件应是（ ）
| 31 |
| 32 |
| A、n≤30 | B、n≤31 |
| C、n≤32 | D、n≤33 |
已知
=（1，2），
=（3，n），若
∥
，则n等于（ ）
| AB |
| CD |
| AB |
| CD |
| A、3 | B、4 | C、5 | D、6 |
已知复数z满足：iz=3+4i（i为虚数单位），则z的共轭复数在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设角α的终边过点P（-4，3），则2sinα+cosα的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
| D、以上都不正确 |
下列说法正确的是（ ）
| A、命题“?x∈R，使得x2+x-1＞0”的否定是“?x∈R，x2+x-1＜0” | ||
B、命题p：“?x∈R，sinx+cosx≤
| ||
| C、“x=-1”是“x2-2x-3=0”的必要不充分条件 | ||
| D、“0＜a＜1”是“函数f（x）=ax（a＞0，a≠1）在R上为减函数”的充要条件 |
已知函数f（x）=x-
，则（ ）
| 1 |
| x |
| A、函数f（x）的定义域是R |
| B、函数f（x）的值域是（-∞，0）∪（0，+∞） |
| C、函数f（x）在其定义域内是奇函数 |
| D、函数f（x）在其定义域内是增函数 |