题目内容
在三角形ABC中,角A、B、C的对边分别为a、b、c,已知asinB=3csinA,c=2,且c,a-1,b+2依次成等比数列.
(1)求a的大小;
(2)求cos(A+
)的值.
(1)求a的大小;
(2)求cos(A+
| π |
| 6 |
考点:两角和与差的余弦函数,等比数列的性质
专题:三角函数的图像与性质
分析:(1)首先,根据正弦定理推论,得到b=3c,然后,根据c,a-1,b+2依次成等比数列.从而确定a的大小;
(2)直接借助于两角和的余弦公式进行求解即可.
(2)直接借助于两角和的余弦公式进行求解即可.
解答:
解:(1)∵asinB=3csinA,
∴ab=3ac,
∴b=3c,∵c=2,
∴b=6,
∵c,a-1,b+2依次成等比数列.
∴(a-1)2=2×8,
∴a=5,
(2)根据余弦定理,得
cosA=
=
=
,
∴sinA=
,
∴cos(A+
)=cosAcos
-sinAsin
=
×
-
×
=
,
∴cos(A+
)=
,
∴ab=3ac,
∴b=3c,∵c=2,
∴b=6,
∵c,a-1,b+2依次成等比数列.
∴(a-1)2=2×8,
∴a=5,
(2)根据余弦定理,得
cosA=
| b2+c2-a2 |
| 2bc |
| 36+4-25 |
| 24 |
| 5 |
| 8 |
∴sinA=
| ||
| 8 |
∴cos(A+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=
| 5 |
| 8 |
| ||
| 2 |
| ||
| 8 |
| 1 |
| 2 |
=
5
| ||||
| 16 |
∴cos(A+
| π |
| 6 |
5
| ||||
| 16 |
点评:本题重点考查了正弦定理、三角恒等变换公式等知识,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知
=(1,2),
=(3,n),若
∥
,则n等于( )
| AB |
| CD |
| AB |
| CD |
| A、3 | B、4 | C、5 | D、6 |
已知函数f(x)=x-
,则( )
| 1 |
| x |
| A、函数f(x)的定义域是R |
| B、函数f(x)的值域是(-∞,0)∪(0,+∞) |
| C、函数f(x)在其定义域内是奇函数 |
| D、函数f(x)在其定义域内是增函数 |
设复数z=
,则
=( )
| 2i |
| 1-i |
. |
| z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|=2
,则k的值为( )
| 3 |
A、k=-
| ||
B、k=-
| ||
C、k=0或k=-
| ||
D、k=0或k=-
|
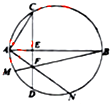 如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.
如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.