题目内容
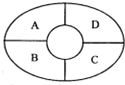如图某综艺节目现场设有A、B、C、D四个观众席，现有由3中不同颜色与2种不同款式组成的6中马甲安排给现场观众，要求每个观众席上的马甲相同，相邻观众席上的马甲的颜色与款式都不相同，则不同的安排方法种数为（ ）| A、72 | B、96 | C、36 | D、48 |
考点：计数原理的应用
专题：排列组合
分析：根据分类和分步计数原理，分AC同色和AC异色两类，然后再分步计算可得．
解答：
解：第一步确定马甲的款式，有2种不同的方法，
第二步确定马甲的颜色，若AC同色，则有
×2×2=12种方法，若AC异色，则有
×1×1=6种方法，
所以确定马甲的颜色有12+6=18种方法，
由分步计数原理知不同的安排方法种数为2×18=36．
故选：C．
第二步确定马甲的颜色，若AC同色，则有
| C | 1 3 |
| A | 2 3 |
所以确定马甲的颜色有12+6=18种方法，
由分步计数原理知不同的安排方法种数为2×18=36．
故选：C．
点评：本题主要考查了分步和分类计数原理，关键是如何分步和分类，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
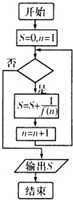
已知函数 f（x）=x2+x，执行如图所示的程序框图，若输出的结果是
，则判断框中的条件应是（ ）
| 31 |
| 32 |
| A、n≤30 | B、n≤31 |
| C、n≤32 | D、n≤33 |
下列说法正确的是（ ）
| A、命题“?x∈R，使得x2+x-1＞0”的否定是“?x∈R，x2+x-1＜0” | ||
B、命题p：“?x∈R，sinx+cosx≤
| ||
| C、“x=-1”是“x2-2x-3=0”的必要不充分条件 | ||
| D、“0＜a＜1”是“函数f（x）=ax（a＞0，a≠1）在R上为减函数”的充要条件 |
已知函数f（x）=x-
，则（ ）
| 1 |
| x |
| A、函数f（x）的定义域是R |
| B、函数f（x）的值域是（-∞，0）∪（0，+∞） |
| C、函数f（x）在其定义域内是奇函数 |
| D、函数f（x）在其定义域内是增函数 |
若tanα=3，则cos2α等于（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
设复数z=
，则
=（ ）
| 2i |
| 1-i |
. |
| z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
直线y=kx+3与圆（x-3）2+（y-2）2=4相交于M，N两点，若|MN|=2
，则k的值为（ ）
| 3 |
A、k=-
| ||
B、k=-
| ||
C、k=0或k=-
| ||
D、k=0或k=-
|