题目内容
定义在R上的函数f（x）满足f（x-2）是偶函数，且对任意x∈R恒有f（3-x）+f（x-1）=2014，又f（4）=2013，则f（2014）= ．
考点：抽象函数及其应用,函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：运用偶函数的定义，将x换为-x，再根据?x∈R，有f（3-x）+f（x-1）=2014，得到f（x+4）+f（x-2）=2014，将x换为x+2，再将x换为x+6，得到函数f（x）的最小正周期为12，从而得到f（2014）=f（-2），再令x=-1，代入f（3-x）+f（x-1）=2014可得f（-2）=1，从而可得结论．
解答：
解：∵定义在R上的函数f（x）满足f（x-2）是偶函数，
∴f（-x-2）=f（x-2），
∵?x∈R，有f（3-x）+f（x-1）=2014，
∴f（4-x）+f（x-2）=2014，
∴f（4-x）+f（-2-x）=2014，
即f（x+4）+f（x-2）=2014，
将x换为x+2，得f（x+6）+f（x）=2014，
将x换为x+6，得f（x+12）+f（x+6）=2014，
∴f（x+12）=f（x），
即函数f（x）的最小正周期为12，
∴f（2014）=f（12×167+10）=f（10）=f（-2），
又∵?x∈R，有f（3-x）+f（x-1）=2014，
令x=-1，得f（4）+f（-2）=2014，
∵f（4）=2013，∴f（-2）=1，
∴f（2014）=1．
故答案为：1．
∴f（-x-2）=f（x-2），
∵?x∈R，有f（3-x）+f（x-1）=2014，
∴f（4-x）+f（x-2）=2014，
∴f（4-x）+f（-2-x）=2014，
即f（x+4）+f（x-2）=2014，
将x换为x+2，得f（x+6）+f（x）=2014，
将x换为x+6，得f（x+12）+f（x+6）=2014，
∴f（x+12）=f（x），
即函数f（x）的最小正周期为12，
∴f（2014）=f（12×167+10）=f（10）=f（-2），
又∵?x∈R，有f（3-x）+f（x-1）=2014，
令x=-1，得f（4）+f（-2）=2014，
∵f（4）=2013，∴f（-2）=1，
∴f（2014）=1．
故答案为：1．
点评：本题主要考查函数的奇偶性和周期性及其运用，考查解决抽象函数的常用方法：赋值法，正确赋值是解决此类问题的关键，务必掌握．
练习册系列答案
相关题目
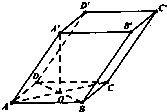如图四棱柱ABCD-A′B′C′D′的底面是正方形，O是底面的中心，A′O=1，AB=AA′=A′D=A′B=