题目内容
已知函数f(x)=
,k>0.
(1)试判断f(x)的奇偶性,并写出其单调增区间;
(2)若不等式f[log2(4x+16)]+f(t-x)>0恒成立,求t的取值范围;
(3)若关于x的方程f(x)=x恰有一根,求实数k的取值范围.
| kx |
| |x|+1 |
(1)试判断f(x)的奇偶性,并写出其单调增区间;
(2)若不等式f[log2(4x+16)]+f(t-x)>0恒成立,求t的取值范围;
(3)若关于x的方程f(x)=x恰有一根,求实数k的取值范围.
考点:函数奇偶性的判断,函数恒成立问题
专题:函数的性质及应用
分析:(1)根据函数奇偶性的定义即可试判断f(x)的奇偶性,并写出其单调增区间;
(2)将不等式f[log2(4x+16)]+f(t-x)>0恒成立,结合函数的奇偶性和单调性,求t的取值范围;
(3)若关于x的方程f(x)=x恰有一根,建立条件关系即可求实数k的取值范围.
(2)将不等式f[log2(4x+16)]+f(t-x)>0恒成立,结合函数的奇偶性和单调性,求t的取值范围;
(3)若关于x的方程f(x)=x恰有一根,建立条件关系即可求实数k的取值范围.
解答:
解:(1)∵函数的定义域为R,
∴f(-x)=-
=-f(x),k>0.
即f(x)是奇函数,
当x=0时,f(0)=0,
当x>0时,f(x)=
=
=k-
,此时函数单调递增,且此时f(x)>0,
当x<0时,f(x)=
=
=
=-k-
,此时函数单调递增,且f(x)<0,
综上函数在R上单调递增,即函数的单调递增区间为(-∞,+∞).
(2)∵f[log2(4x+16)]+f(t-x)>0,
∴f[log2(4x+16)]>-f(t-x)=f(x-t),
∵函数在R上单调递增,
∴不等式恒成立等价为[log2(4x+16)>x-t,
即4x+16>2x-t=2x•2-t恒成立,
即2t>
=
恒成立.
∵g(x)=
≤
=
=
,
当且仅当2x=
,即2x=4,x=2时取等号,
∴2t>
=2-3,
∴t>-3,
即t的取值范围是t>-3;
(3)由f(x)=
=x,k>0.
即x(
-1)=0,
若关于x的方程f(x)=x恰有一根,
则
-1≠0,即y=k与y=1+|x|没有公共点,
即0<k<1,即实数k的取值范围是0<k<1.
∴f(-x)=-
| kx |
| |x|+1 |
即f(x)是奇函数,
当x=0时,f(0)=0,
当x>0时,f(x)=
| kx |
| x+1 |
| k(x+1)-k |
| x+1 |
| k |
| x+1 |
当x<0时,f(x)=
| kx |
| |x|+1 |
| kx |
| -x+1 |
| k(x-1)+k |
| -(x-1) |
| k |
| x-1 |
综上函数在R上单调递增,即函数的单调递增区间为(-∞,+∞).
(2)∵f[log2(4x+16)]+f(t-x)>0,
∴f[log2(4x+16)]>-f(t-x)=f(x-t),
∵函数在R上单调递增,
∴不等式恒成立等价为[log2(4x+16)>x-t,
即4x+16>2x-t=2x•2-t恒成立,
即2t>
| 2x |
| 4x+16 |
| 1 | ||
2x+
|
∵g(x)=
| 1 | ||
2x+
|
| 1 | ||||
2
|
| 1 | ||
2
|
| 1 |
| 8 |
当且仅当2x=
| 16 |
| 2x |
∴2t>
| 1 |
| 8 |

∴t>-3,
即t的取值范围是t>-3;
(3)由f(x)=
| kx |
| |x|+1 |
即x(
| k |
| |x|+1 |
若关于x的方程f(x)=x恰有一根,
则
| k |
| |x|+1 |
即0<k<1,即实数k的取值范围是0<k<1.
点评:本题主要考查函数奇偶性和单调性的判断,以及不等式恒成立问题,综合性较强,运算量较大,有一定的难度.

练习册系列答案
相关题目
某工厂有甲、乙、丙三类产品,其数量之比为1:2:4,现要用分层抽样的方法从中抽取140件产品进行质量检测,则乙类产品应抽取的件数为( )
| A、20 | B、40 | C、60 | D、80 |
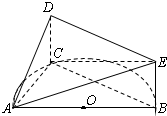 如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB=
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB= 在直四棱柱ABCD-A1B1C1D1中,AB⊥BC,AD∥BC,AA1=BC=2,AB=
在直四棱柱ABCD-A1B1C1D1中,AB⊥BC,AD∥BC,AA1=BC=2,AB=