题目内容
已知集合A={x|a+1＜x＜2a-3}，B={x|x≥3}，且满足A⊆B，求实数a的取值范围．
考点：集合的包含关系判断及应用
专题：集合
分析：首先，对集合A进行讨论，分为空集和不是空集两种情形，然后，借助于条件A⊆B，确定a的取值范围．
解答：
解：当A=∅时，即a+1≥2a-3，
∴a≤4，
∵∅⊆B，
∴符合题意，
当A≠∅时，即a+1＜2a-3，
∴a＞4，
∵A⊆B，
∴a+1≥3，
∴a≥2，
∵a＞4，
∴a＞4，
∴a∈（-∞，+∞）．
∴a≤4，
∵∅⊆B，
∴符合题意，
当A≠∅时，即a+1＜2a-3，
∴a＞4，
∵A⊆B，
∴a+1≥3，
∴a≥2，
∵a＞4，
∴a＞4，
∴a∈（-∞，+∞）．
点评：本题务必注意集合A的元素取值情况，属于中档题，难度中等．
练习册系列答案
名校课堂系列答案
相关题目
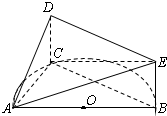如图，AB是半圆O的直径，C是半圆O上除A、B外的一个动点，DC垂直于半圆O所在的平面，DC∥EB，DC=EB，AB=4，tan∠EAB=