题目内容
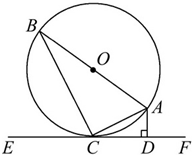 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.(1)求证:∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求弧AC的长.
考点:与圆有关的比例线段
专题:直线与圆
分析:(1)由已知得∠ACD=∠ABC,∠ACB=∠ADC=90°,由此能证明∠BAC=∠CAD.
(2)由∠B=30°,AB=12,由此能求出弧AC的长.
(2)由∠B=30°,AB=12,由此能求出弧AC的长.
解答:
(1)证明:∵AB是⊙O的直径,AC是弦,
直线EF是过点C的⊙O的切线,AD⊥EF于点D,
∴∠ACD=∠ABC,∠ACB=∠ADC=90°
∴∠BAC=∠CAD.
(2)解:∵∠B=30°,AB=12,
∴弧AC的长=
×2π×(
)2=π.
直线EF是过点C的⊙O的切线,AD⊥EF于点D,
∴∠ACD=∠ABC,∠ACB=∠ADC=90°
∴∠BAC=∠CAD.
(2)解:∵∠B=30°,AB=12,
∴弧AC的长=
| 30° |
| 360° |
| 12 |
| 2 |
点评:本题考查两角相等的证明,考查弧长的求法,是中档题,解题时要认真审题.

练习册系列答案
相关题目
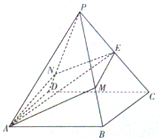 如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).
如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).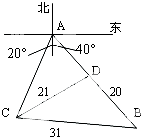 观测站C处在目标A的南偏西20°方向,从A出发有一条南偏东40°走向的公路,在C处观测到与C相距31km公路上的B处有一人正沿此公路向A走去,走20km到达D处,此时测得CD距离21km,求此人在D处距A还有多远?
观测站C处在目标A的南偏西20°方向,从A出发有一条南偏东40°走向的公路,在C处观测到与C相距31km公路上的B处有一人正沿此公路向A走去,走20km到达D处,此时测得CD距离21km,求此人在D处距A还有多远?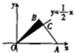 如图,等腰三角形OAB的顶点A,B的坐标分别为(6,0),(3,3),AB与直线y=
如图,等腰三角形OAB的顶点A,B的坐标分别为(6,0),(3,3),AB与直线y=