题目内容
已知实数a<0,函数f(x)=
若f(1-a)=f(1+a),则a的值为 .
|
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:由分段函数的表达式,及a<0,得1-a>1,1+a<1,则f(1-a)=f(1+a)即有-(1-a)-2a=2(1+a)+a,
解出a即可.
解出a即可.
解答:
解:由于函数f(x)=
,
则由实数a<0,得1-a>1,1+a<1,
则f(1-a)=f(1+a)即有-(1-a)-2a=2(1+a)+a,
解得a=-
.
故答案为:-
.
|
则由实数a<0,得1-a>1,1+a<1,
则f(1-a)=f(1+a)即有-(1-a)-2a=2(1+a)+a,
解得a=-
| 3 |
| 4 |
故答案为:-
| 3 |
| 4 |
点评:本题考查分段函数及运用,考查分段函数值应注意各段的自变量的范围,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
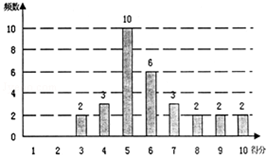 下列命题:
下列命题: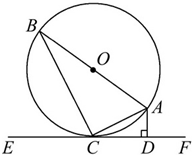 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.