题目内容
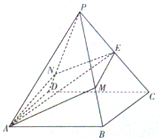 如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).
如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).(Ⅰ)当M是PB的中点时,求PN的长;
(Ⅱ)求直线AE与平面PBC所成角的正弦值.
考点:直线与平面所成的角
专题:综合题,空间角
分析:(Ⅰ)当M是PB的中点时,证明ME∥AN,可得N、D两点重合,即可求PN的长;
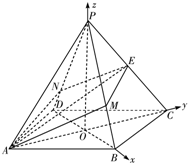
(Ⅱ)连接AC、BD交于点O,以O为坐标原点建立如图所示的空间直角坐标系,求出平面PBC的一个法向量,利用向量的夹角公式,即可求直线AE与平面PBC所成角的正弦值.
(Ⅱ)连接AC、BD交于点O,以O为坐标原点建立如图所示的空间直角坐标系,求出平面PBC的一个法向量,利用向量的夹角公式,即可求直线AE与平面PBC所成角的正弦值.
解答:
 解:(Ⅰ)当M是PB的中点时,ME∥BC.
解:(Ⅰ)当M是PB的中点时,ME∥BC.
因为BC∥平面PAD,所以ME∥平面PAD,
所以ME∥AN.
又ME∥AD,所以N、D两点重合.
所以PN=PD=
=
.…(4分)
(Ⅱ)连接AC、BD交于点O,以O为坐标原点建立如图所示的空间直角坐标系,则B(
,0,0),C(0,
,0),P(0,0,3),A(0,-
,0),E(0,
,
)
∴
=(
,0,-3),
=(0,
,-3),
=(0,
,
).…(6分)
设平面PBC的一个法向量为
=(x,y,z),则
,令z=
,得
=(3,3,
).…(8分)
设直线AE与平面PBC所成的角为θ,则sin θ=|cos?m,
>|=
=
.
所以直线AE与平面PBC所成角的正弦值为
.…(12分)
 解:(Ⅰ)当M是PB的中点时,ME∥BC.
解:(Ⅰ)当M是PB的中点时,ME∥BC.因为BC∥平面PAD,所以ME∥平面PAD,
所以ME∥AN.
又ME∥AD,所以N、D两点重合.
所以PN=PD=
32+(
|
| 11 |
(Ⅱ)连接AC、BD交于点O,以O为坐标原点建立如图所示的空间直角坐标系,则B(
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∴
| PB |
| 2 |
| PC |
| 2 |
| AE |
3
| ||
| 2 |
| 3 |
| 2 |
设平面PBC的一个法向量为
| m |
|
| 2 |
| m |
| 2 |
设直线AE与平面PBC所成的角为θ,则sin θ=|cos?m,
| AE |
| ||||||||
|
2
| ||
| 15 |
所以直线AE与平面PBC所成角的正弦值为
2
| ||
| 15 |
点评:本题考查了面面垂直的证明,考查线面角,考查向量知识的运用,正确求出平面的法向量是关键.

练习册系列答案
相关题目
如图,在△ABC中,
=2
,记
=
,
=
,则
=( )

| CD |
| DB |
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
下列命题中错误的是( )
| A、命题“若p则q”与命题“若¬q则¬p”互为逆否命题 |
| B、命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,p∨q为真 |
| C、若p∨q为假命题,则p、q均为假命题 |
| D、“若am2=bm2”,则a<b的逆命题为真命题 |
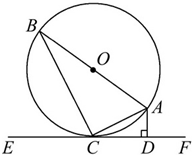 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.