题目内容
某品牌汽车的4S店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
已知分3期付款的频率为0.15,并且4S店销售一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元,以频率作为概率.
(Ⅰ)求事件A:“购买该品牌汽车的3位顾客中,至多有1位分4期付款”的概率;
(Ⅱ)用X表示销售一辆该品牌汽车的利润,求X的分布列及数学期望E(x)
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 35 | 25 | a | 10 | b |
(Ⅰ)求事件A:“购买该品牌汽车的3位顾客中,至多有1位分4期付款”的概率;
(Ⅱ)用X表示销售一辆该品牌汽车的利润,求X的分布列及数学期望E(x)
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)由
=0.15,得a=15,b=15,由此能求出“购买该品牌汽车的3位顾客中至多有1位采用4期付款”的概率.
(Ⅱ)记分期付款的期数为ξ,X的可能取值为1,1.5,2,分别求出相应的概率,由此能求出X的分布列和X的数学期望.
| a |
| 100 |
(Ⅱ)记分期付款的期数为ξ,X的可能取值为1,1.5,2,分别求出相应的概率,由此能求出X的分布列和X的数学期望.
解答:
解:(Ⅰ)由
=0.15,得a=15,
因为35+25+a+10+b=100,所以b=15,
“购买该品牌汽车的3位顾客中至多有1位采用4期付款”的概率:P(A)=0.93+
×0.1×(1-0.1)2=0.972.…(4分)
(Ⅱ)记分期付款的期数为ξ,
依题意得P(ξ=1)=0.35,P(ξ=2)=0.25,
P(ξ=3)=0.15,P(ξ=4)=0.1,P(ξ=5)=0.15,…(6分)
因为X的可能取值为1,1.5,2,
并且P(X=1)=P(ξ=1)=0.35,
P(X=1.5)=P(ξ=2)+P(ξ=3)=0.4,
P(X=2)=P(ξ=4)+P(ξ=5)=0.1+0.15=0.25.…(10分)
所以X的分布列为
所以X的数学期望为E(X)=1×0.35+1.5×0.4+2×0.25=1.45(万元).…(12分)
| a |
| 100 |
因为35+25+a+10+b=100,所以b=15,
“购买该品牌汽车的3位顾客中至多有1位采用4期付款”的概率:P(A)=0.93+
| C | 1 3 |
(Ⅱ)记分期付款的期数为ξ,
依题意得P(ξ=1)=0.35,P(ξ=2)=0.25,
P(ξ=3)=0.15,P(ξ=4)=0.1,P(ξ=5)=0.15,…(6分)
因为X的可能取值为1,1.5,2,
并且P(X=1)=P(ξ=1)=0.35,
P(X=1.5)=P(ξ=2)+P(ξ=3)=0.4,
P(X=2)=P(ξ=4)+P(ξ=5)=0.1+0.15=0.25.…(10分)
所以X的分布列为
| X | 1 | 1.5 | 2 |
| P | 0.35 | 0.4 | 0.25 |
点评:本题考查离散型随机变量的数学期望和方差的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
相关题目
△ABC中,若a=3,c=7,∠C=60°,则边长b为( )
| A、5 | B、8 |
| C、5或-8 | D、-5或8 |
设等比数列{an}的前n项和为Sn,若S1=
a2-
,S2=
a3-
,则公比q=( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、1 | B、4 | C、4或0 | D、8 |
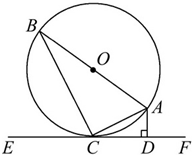 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.