题目内容
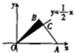 如图,等腰三角形OAB的顶点A,B的坐标分别为(6,0),(3,3),AB与直线y=
如图,等腰三角形OAB的顶点A,B的坐标分别为(6,0),(3,3),AB与直线y=| 1 |
| 2 |
考点:几何概型
专题:计算题,概率与统计
分析:求出直线AB的方程与直线y=
x交于点C(4,2),再求出面积,即可求出点P落在阴影部分的概率.
| 1 |
| 2 |
解答:
解:A,B的坐标分别为(6,0),(3,3),方程为y=-x+6,与直线y=
x交于点C(4,2),
∴阴影部分的面积为
×3×6-
×2×6=3,
∵等腰三角形OAB的面积为
×3×6=9,
∴点P落在阴影部分的概率为P=
=
.
故答案为:
.
| 1 |
| 2 |
∴阴影部分的面积为
| 1 |
| 2 |
| 3 |
| 2 |
∵等腰三角形OAB的面积为
| 1 |
| 2 |
∴点P落在阴影部分的概率为P=
| 3 |
| 9 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查点P落在阴影部分的概率,考查学生的计算能力,确定面积是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
下列命题中错误的是( )
| A、命题“若p则q”与命题“若¬q则¬p”互为逆否命题 |
| B、命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,p∨q为真 |
| C、若p∨q为假命题,则p、q均为假命题 |
| D、“若am2=bm2”,则a<b的逆命题为真命题 |
若点(x,y)在映射f下的象为点(2x,x-y),则(-1,2)在映射f下的原象为( )
| A、(-2,-3) | ||||
| B、(-2,1) | ||||
C、(
| ||||
D、(-
|
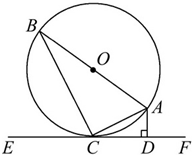 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.