题目内容
对于函数f(x)与g(x)和区间D,如果存在唯一x0∈D,使|f(x0)-g(x0)|≤2,则称函数f(x)与g(x)在区间D上的“友好函数”.现给出两个函数:
①f(x)=x2,g(x)=2x-4;
②f(x)=2
,g(x)=x+3;
③f(x)=e-x,g(x)=-
;
④f(x)=lnx,g(x)=x+1,
则函数f(x)与g(x)在区间(0,+∞)上为“友好函数”的是 .(填正确的序号)
①f(x)=x2,g(x)=2x-4;
②f(x)=2
| x |
③f(x)=e-x,g(x)=-
| 1 |
| x |
④f(x)=lnx,g(x)=x+1,
则函数f(x)与g(x)在区间(0,+∞)上为“友好函数”的是
考点:函数的值
专题:函数的性质及应用
分析:对照新定义,利用配方法、导数法可确定函数的值域,由此,就可以得出结论.
解答:
解:对于①,f(x)-g(x)=x2-2x+4=(x-1)2+3≥3,
∴不存在x0∈(0,+∞),使|f(x0)-g(x0)|≤2,∴①不是“友好函数”;
对于②,g(x)-f(x)=x-2
+3=(
-1)2+2≥2,
当且仅当x=1时,|g(x)-f(x)|≤2.∴②是“友好函数”;
对于③,h(x)=f(x)-g(x)=e-x+
,
h′(x)=-e-x-
<0,
∴函数h(x)在(0,+∞)上单调减,
∴x→0,h(x)→+∞,x→+∞,h(x)→0,
使|f(x0)-g(x0)|≤2的x0不唯一,∴③不是“友好函数”;
对于④,h(x)=g(x)-f(x)=x-lnx+1(x>0),
h′(x)=1-
,
令h′(x)>0,可得x>1,令h′(x)<0,可得0<x<1,
∴x=1时,函数取得极小值,且为最小值,最小值为h(1)=2,
∴g(x)-f(x)≥2,
使|f(x0)-g(x0)|≤2的x0唯一,∴④是“友好函数”.
故答案为:②④.
∴不存在x0∈(0,+∞),使|f(x0)-g(x0)|≤2,∴①不是“友好函数”;
对于②,g(x)-f(x)=x-2
| x |
| x |
当且仅当x=1时,|g(x)-f(x)|≤2.∴②是“友好函数”;
对于③,h(x)=f(x)-g(x)=e-x+
| 1 |
| x |
h′(x)=-e-x-
| 1 |
| x2 |
∴函数h(x)在(0,+∞)上单调减,
∴x→0,h(x)→+∞,x→+∞,h(x)→0,
使|f(x0)-g(x0)|≤2的x0不唯一,∴③不是“友好函数”;
对于④,h(x)=g(x)-f(x)=x-lnx+1(x>0),
h′(x)=1-
| 1 |
| x |
令h′(x)>0,可得x>1,令h′(x)<0,可得0<x<1,
∴x=1时,函数取得极小值,且为最小值,最小值为h(1)=2,
∴g(x)-f(x)≥2,
使|f(x0)-g(x0)|≤2的x0唯一,∴④是“友好函数”.
故答案为:②④.
点评:本题考查“友好函数”的判断,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
设等比数列{an}的前n项和为Sn,若S1=
a2-
,S2=
a3-
,则公比q=( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、1 | B、4 | C、4或0 | D、8 |
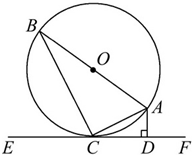 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.